押さえておきたい∑(シグマ)の応用計算４パターン(和の和,nを含む数列,分数,等差×等比)

$\sum$ の応用問題の中でも頻出の重要パターンを扱います。難しい問題もありますが，ポイントを押さえて，確実に解けるようにしよう。難関大を目指すなら，このレベルの問題が解けることがスタートラインです。中堅を目指すなら，このレベルの問題で差がつきます。

第 $k$ 項が和の形で表される数列の和（和の和）

問題

解説（授業）

等差数列もしくは等比数列の和であれば，それぞれの和の公式で求められますが，それ以外の場合は$\sum$ を利用して求めるしかありません。そのために必要なことは，第 $k$ 項 $a_k$ を求めることです。

数列を見てみましょう。

$1，1+2，1+2+4，\cdots$

第 $k$ 項を $a_k$ とすると，
$a_1=1$
$a_2=1+2$
$a_3=1+2+2^2$
どんな規則があるか考えながら見ましょう。同じ規則で書いてみると
$a_4=1+2+2^2+2^3$
$a_5=1+2+2^2+2^3+2^4$
となりますね。よって，
$a_k=1+2+2^2+\cdots+2^{k-1}$
であることが分かります。

これは，等比数列の和ですね。
等比数列の和の求め方は覚えていますか？何が必要でしたか？
はい、「初項」「公比」「項数」の $3$ つでしたね。

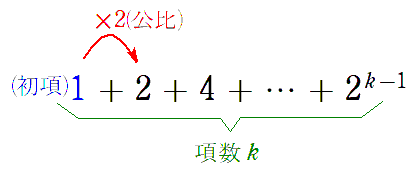
$a_k$ は初項 $1$，公比 $2$，項数 $k$ の等比数列の和より

$a_k=1\times\displaystyle\frac{2^k-1}{2-1}$
よって，
$a_k=2^k-1$
が得られました。あとは，これを $\sum$ に入れて計算するだけです。

求める和は，
$\displaystyle\sum_{k=1}^{n}{a_k}=\displaystyle\sum_{k=1}^{n}{(2^k-1)}$

バラバラにしましょう。
$\displaystyle\sum_{k=1}^{n}{(2^k-1)}=$ $\displaystyle\sum_{k=1}^{n}{2^k}$ $-$ $\displaystyle\sum_{k=1}^{n}{1}$

$\displaystyle\sum_{k=1}^{n}{1}=1\times n=n$ は簡単ですね。

$\displaystyle\sum_{k=1}^{n}{2^k}$ は等比数列の和で求めるんでしたね。

$\displaystyle\sum_{k=1}^{n}{2^k}$ は初項 $2$，公比 $2$，項数 $n$ の等比数列の和で計算できますね。

$\displaystyle\sum_{k=1}^{n}{2^k}$ $-\displaystyle\sum_{k=1}^{n}{1}$ $=$ $2\times\displaystyle\frac{2^n-1}{2-1}$ $-$ $n$

あとは計算するだけです。特にややこしい部分もありません。

$2\times\displaystyle\frac{2^n-1}{2-1}$ $-$ $n$ $=2^{n+1}-n-2$　(答)

等比数列の和の公式を繰り返し用いることで求めることができました。公式がしっかり入っていないと難しい問題ですね。等比数列の和の公式が怪しいという人は以下の記事で確認しておきましょう。

答案

第 $k$ 項を $a_k$ とすると，
$a_k=1+2+4+\cdots+2^{k-1}$
[初項 $1$，公比 $2$，項数 $k$ の等比の和]

$a_k=1\times\displaystyle\frac{2^k-1}{2-1}$
　 $=2^k-1$

よって，求める和は
　$\displaystyle\sum_{k=1}^{n}{a_k}$

$=\displaystyle\sum_{k=1}^{n}{(2^k-1)}$

$=$$\displaystyle\sum_{k=1}^{n}{2^k}$$-\displaystyle\sum_{k=1}^{n}{1}$
[$\displaystyle\sum_{k=1}^{n}{2^k}$ は初項 $2$，公比 $2$，項数 $n$ の等比の和]

$=$ $2\times\displaystyle\frac{2^n-1}{2-1}$ $-$ $n$

$=2^{n+1}-n-2$　(答)

第 $k$ 項に $n$ が含まれる数列の和

問題

解説（授業）

第 $k$ 項 $a_k$ を求める( $k$ で表す)のが基本方針でしたね。第 $k$ 項を $a_k$ とすると，
$a_1=1^{2}\cdot n$
$a_2=2^{2}\cdot (n-1)$
$a_3=3^{2}\cdot (n-2)$
この時点で $a_k$ が分かる人もいるかもしれませんが，分からないという人もいると思うので一緒に確認しましょう。

ややこしいので左側と右側に分けて規則を調べます。

左側は，
$1^2，2^2，3^2，･･･$
なので，$k$ 番目は $k^2$ とすぐ分かりますね。

右側は，少しややこしい
$n，n-1，n-2，･･･$
こんなふうに見てみましょう。
1 番目　$n$ $-$ $0$
2 番目　$n$ $-$ $1$
3 番目　$n$ $-$ $2$
　$\cdots$
$k$ 番目　$n$ $-$ $(k-1)$

変化している部分に着目するのがポイントです。

右側は，以下のように考える方法もありますね。
$n，n-1，n-2，\cdots$ は，
初項 $n$，公差 $-1$ の等差数列より,
$k$ 番目は，
$n+(k-1)\times(-1)$
[初項 $n$ に公差 $-1$ を $(k-1)$ 回足したもの]

このように等差数列とみなす考え方は，さらに複雑になって規則から書くのが難しい場合でも計算により求められます。ただし，等差数列の一般項についての理解が十分にないと難しいでしょう。理解が甘いと感じた場合は，下記の記事を確認しておこう。

これにより，第 $k$ 項 $a_k$ は，
$a_k$ $=$ $k^2$ $\cdot$ $\left\{n-(k-1)\right\}$
　 $=k^2(n-k+1)$
　 $=-k^3+(n+1)k^2$
[ $k$ について整理しておいた]

よって，求める和は
$\displaystyle\sum_{k=1}^{n}{\left\{-k^3+(n+1)k^2\right\}}$

あとは，この和の計算をするだけですが，慣れていないと戸惑いますね。
戸惑う人の理由は $\sum$ の中に $n$ が入っていて，どう処理すればいいのか分からないからでしょう。これは次のことを知っていれば(理解していれば)難しくありません。

『$\displaystyle\sum_{k=\text{□}}^{\text{◯}}$ においては，$k$ 以外の文字はすべて定数とみなす。』

つまり， 今回 $n$ を定数として扱うということです。理由は分かりますか？

例えば，

$\displaystyle\sum_{k=1}^{n}{nk}$ $=n\displaystyle\sum_{k=1}^{n}{k}$
　[定数は外に出せる]

とできるということだけど，実際，

　$\displaystyle\sum_{k=1}^{n}{nk}$

$=n\times1+n\times2+n\times3+\cdots+n\times n$

$=n\times(1+2+3+\cdots+n)$

$=n\times\displaystyle\sum_{k=1}^{n}{k}$

となって成り立ちます。そもそも $\displaystyle\sum_{k=1}^{n}$ の定義は 『$k$ に $1$ から $n$ まで代入して足す』でしたね。変化するのは $k$ だけなので，他の文字は定数とみなせるということです。$\sum$ の定義を考えたら当たり前ですね。

結局，今回の場合，

$\displaystyle\sum_{k=1}^{n}{(n+1)k^2}$ $=(n+1)\displaystyle\sum_{k=1}^{n}{k^2}$

として計算できるかどうかがすべてです。あとは $\sum$ の公式を使って慎重に計算しましょう。

ちなみに，$-k^3+(n+1)k^2$ のように $k$ で整理したのは，$n$ は定数扱いで $\sum$ の外に出すことを見越しているからですね。

$\displaystyle\sum_{k=1}^{n}{\left\{-k^3+(n+1)k^2\right\}}$

$=-\displaystyle\sum_{k=1}^{n}{k^3}+$ $(n+1)\displaystyle\sum_{k=1}^{n}{k^2}$

$\sum$ の公式を適用して

$=-\displaystyle\frac{1}{4}n^2\left(n+1\right)^2$

　$+(n+1)\times\displaystyle\frac{1}{6}n(n+1)(2n+1)$

$=-\displaystyle\frac{1}{4}n^2\left(n+1\right)^2+\displaystyle\frac{1}{6}n(n+1)^2(2n+1)$

$\displaystyle\frac{1}{12}n(n+1)^2$ でくくって

$=\displaystyle\frac{1}{12}n(n+1)^2\left\{-3n+2(2n+1)\right\}$

$=\displaystyle\frac{1}{12}n(n+1)^2(n+2)$　(答)

答案

第 $k$ 項を $a_k$ とする。

$1^2，2^2，3^2，\cdots$ に着目すると，
$k$ 番目は $k^2$

$n，n-1，n-2，\cdots$ に着目すると，
$k$ 番目は $n-(k-1)$

よって，
$a_k=$ $k^2$ $\cdot$ $\left\{n-(k-1)\right\}$
　 $=k^2(n-k+1)$
　 $=-k^3+(n+1)k^2$

したがって，求める和は，
　$\displaystyle\sum_{k=1}^{n}{a_k}$

$=\displaystyle\sum_{k=1}^{n}{\left\{-k^3+(n+1)k^2\right\}}$

$=-\displaystyle\sum_{k=1}^{n}{k^3}+(n+1)\displaystyle\sum_{k=1}^{n}{k^2}$

$=-\displaystyle\frac{1}{4}n^2\left(n+1\right)^2$

　$+(n+1)\times\displaystyle\frac{1}{6}n(n+1)(2n+1)$

$=-\displaystyle\frac{1}{4}n^2\left(n+1\right)^2+\displaystyle\frac{1}{6}n(n+1)^2(2n+1)$

$=\displaystyle\frac{1}{12}n(n+1)^2\left\{-3n+2(2n+1)\right\}$

$=\displaystyle\frac{1}{12}n(n+1)^2(n+2)$　(答)

$\sum$ の公式が使えない式の和の計算（部分分数分解や有理化の利用）

問題

解説（授業）

　今回は $\sum$ の公式が使えないので，工夫して計算する必要があります。このとき，考えて欲しいのは「差(厳密に言うと階差)の形」にできないかということです。

　$f(k)-f(k+1)$ などの形にすることができれば，$k$ に $1$ から $n$ まで代入して足すと，以下のように打ち消し合う部分が現れます。あとは，どこが残るのかを慎重に考えて書くだけです。このとき，残る部分が必ず左右対称になることを意識するとミスしにくくなります。

　差の形を作る方法はいくつかありますが「部分分数分解」と「有理化」を頭に入れておきましょう。ハイレベルな問題を解いているとこれ以外のパターンもありますが，根底にあるのは「差を作る」ということです。医学部や難関大を目指すのであれば，差を作る意識が重要になってきます。それ以外の人であれば，分数だったら部分分数分解，√(ルート) があれば有理化くらいの認識でもほぼ問題ありません。

　部分分数分解は，数学Ⅱの「式と証明」の内容ですが，ここで説明を始めると完全に脱線するため，細かい話は割愛します。部分分数分解が分からないという人は，ひとまず，以下の公式を適用すればいいと考えて下さい。( $\sum$ の計算においてはこれで十分であり，むしろ実践的。)

　$\displaystyle\frac{1}{AB}=\displaystyle\frac{1}{B-A}\left(\displaystyle\frac{1}{A}-\displaystyle\frac{1}{B}\right)$

　$\displaystyle\frac{1}{ABC}=\displaystyle\frac{1}{BC-AB}\left(\displaystyle\frac{1}{AB}-\displaystyle\frac{1}{BC}\right)$

前置きが長くなりましたが，実際に問題を解いていきましょう。

$\displaystyle\sum_{k=1}^{n}{\displaystyle\frac{1}{4k^2-1}}$

部分分数分解をするため，まず分母を因数分解します。

$\displaystyle\frac{1}{4k^2-1}=\displaystyle\frac{1}{(2k-1)(2k+1)}$

細かいことになりますが，因数分解するとき $(2k+1)(2k-1)$ と $(2k-1)(2k+1)$ では，当然どちらでも問題ありませんが，小さい方 (今回は $2k-1$）から先に書くようにすると，部分分数分解か若干しやすくなります。

それでは，さっきの公式 $\displaystyle\frac{1}{AB}=\displaystyle\frac{1}{B-A}\left(\displaystyle\frac{1}{A}-\displaystyle\frac{1}{B}\right)$ を適用して部分分数分解をしましょう。

　$\displaystyle\frac{1}{(2k-1)(2k+1)}$

　[数式切れていたら横スクロール]

$=\displaystyle\frac{1}{2}\left(\displaystyle\frac{1}{2k-1}-\displaystyle\frac{1}{2k+1}\right)$

よって，求める和は

$\displaystyle\frac{1}{2}\displaystyle\sum_{k=1}^{n}{\left(\displaystyle\frac{1}{2k-1}-\displaystyle\frac{1}{2k+1}\right)}$

となるので，$\sum$ の定義通り，$k$ に $1$ から $n$ まで代入して足すと，以下のように求まります。

答案

$\displaystyle\sum_{k=1}^{n}{\displaystyle\frac{1}{4k^2-1}}$

$=\displaystyle\sum_{k=1}^{n}{\displaystyle\frac{1}{(2k-1)(2k+1)}}$

$=\displaystyle\frac{1}{2}\displaystyle\sum_{k=1}^{n}{\left(\displaystyle\frac{1}{2k-1}-\displaystyle\frac{1}{2k+1}\right)}$
　[部分分数分解した]

　[$k$ に $1$ から $n$ まで代入して足した(数式切れていたら横スクロール)]

$=\displaystyle\frac{1}{2}\left(1-\displaystyle\frac{1}{2n+1}\right)$
　[打ち消し合う部分を消して残ったものを書いた]

$=\displaystyle\frac{1}{2}\times\displaystyle\frac{2n}{2n+1}$
　[カッコ内を通分して計算した]

$=\displaystyle\frac{n}{2n+1}$　(答)

(等差)×(等比)の和

問題

解説（授業）

応用問題の中でも特に重要な問題です。どうでも良い話かもしれませんが，私は大学受験で３大学（国立２、私立１）受験しましたが，その内の２大学でこのパターンの問題が出題されました(笑)
もちろん偶然ですが，近年でも大学入試でよく出題されているパターンなので，しっかり押さえておきましょう。

最初から脱線してしまいましたが，問題に戻りましょう。公式で求められる形ではなく，部分分数分解や有理化をするような形でもありませんね。今回の形は，見てすぐあることに気付かなくてはなりません。とりあえず，$\sum$ を使わず，具体的に書き出してみます。

$\displaystyle\sum_{k=1}^{n}{2k\cdot3^{k-1}}$

$=$ $2$ $\cdot$ $1$$+$$4$ $\cdot$ $3$$+$$6$ $\cdot$ $3^2$$+$$\cdots$$+$$2n$ $\cdot$ $3^{n-1}$

　左側だけ見ると等差数列，
　右側だけ見ると等比数列
となっていることに気づきましたか？

このような $(\text{等差})$$\times$$(\text{等比})$ となっている数列の和 $S$ は「公比をかけたものを(ずらして)引く」ことで上手く計算できます。パターンとして覚えておこう！

今回の場合，等比数列の公比は $3$ であるから
$S-$$3$$S$ を計算します。（下のように $3S$ の右辺を $1$ つずつずらして書きます）

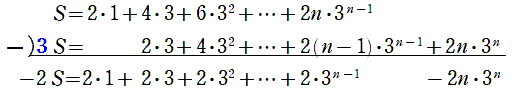
すると，右辺が
$2\cdot1+2\cdot3+2\cdot3^2+$$\cdots+2\cdot3^{n-1}$ $-2n\cdot3^n$
となり，等比数列の和が現れます。また，最後の項が引き算になることに注意してください。

等比数列の和は「初項」「公比」「項数」に着目するんでしたね。

$2\cdot1+2\cdot3+2\cdot3^2+$$\cdots+2\cdot3^{n-1}$ は
初項 $2$，公比 $3$，項数 $n$ の等比数列の和なので，

$2\cdot1+2\cdot3+2\cdot3^2+$$\cdots+2\cdot3^{n-1}$
$=2\times\displaystyle\frac{3^n-1}{3-1}$ $=3^n-1$

よって，
$-2S=3^n-1-2n\cdot3^n$
$3^n$ をまとめて
$-2S=(1-2n)\cdot3^n-1$
$-2$ で割って
$S=-\displaystyle\frac{1}{2}\left\{(1-2n)\cdot3^n-1)\right\}$
$-$ を中に入れて
　$=\displaystyle\frac{1}{2}\left\{(2n-1)\cdot3^n+1)\right\}$　(答)

さて，答えは出せましたが補足説明をしておきます。
　$k$ の１次式を見て等差数列，
　$(\text{定数})^k$ を見て等比数列
であることは瞬時に気付く必要があります。
つまり，($k$ の１次式)×$(\text{定数})^k$ を見たらすぐに今回のパターンと見抜けることが必要です。
もちろん，
$S=$ $2$ $\cdot$ $1$$+$$4$ $\cdot$ $3$$+$$6$ $\cdot$ $3^2$$+$$\cdots$$+$$2n$ $\cdot$ $3^{n-1}$ を求めよ。
のように，和の形で出題されていても気づかなくてはいけません。
掛け算(や分数)の形になっているときは，(等差)×(等比)となっていないか疑う癖をつけておきましょう。

ちなみに，以下のような形もあります。

　$\displaystyle\sum_{k=1}^{n}{\displaystyle\frac{k+1}{2^k}}$

分かりますか？

$\displaystyle\frac{k+1}{2^k}=$$(k+1)$ $\cdot$ $\left(\displaystyle\frac{1}{2}\right)^k$

と見れば，確かに $(\text{等差})$$\cdot$$(\text{等比})$ です。意識しておかないと見逃してしまいますね。

答案

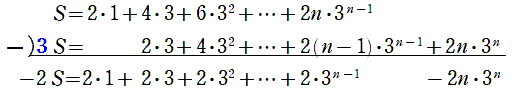
$S-3S$ を計算することにより，

$-2S$ $=$ $2\cdot1+2\cdot3+2\cdot3^2+$
　　　$\cdots+2\cdot3^{n-1}$ $-2n\cdot3^n$
　[下線部が等比の和，最後の項が ｢$-$｣ であることに注意]

$-2S=$ $2\times\displaystyle\frac{3^n-1}{3-1}$ $-2n･3^n$
　[初項 $2$，公比 $3$，項数 $n$ の等比の和]

$-2S=3^n-1-2n\cdot 3^n$

よって，

$-2S=(1-2n)\cdot3^n-1$

したがって，

$S=-\displaystyle\frac{1}{2}\left\{(1-2n)\cdot3^n-1)\right\}$

　$=\displaystyle\frac{1}{2}\left\{(2n-1)\cdot3^n+1)\right\}$　(答)

$\sum$ の応用問題がこれで「解ける！」