(注意) 【~型】はパターンを意識するためであり,当サイト独自の表現です。答案に書かないように。
漸化式の中でも土台となる $4$ パターンについて確認します。漸化式の応用問題は,変形や置き換えにより,このページで扱う $4$ パターンに帰着させる問題がほとんどです。「この形にさえすれば解ける」となるように,しっかり理解して解けるようにしておきましょう。前提として,「等差数列の一般項の求め方」「等比数列の一般項の求め方」「階差数列による一般項の求め方」が頭に入っている必要があります。
一般項の公式から瞬時に求める漸化式3パターン
【等差型】 $a_{n+1}=a_n+$ $d$
公差 $d$ の等差数列
【等比型】 $a_{n+1}=$ $r$ $a_n$
公比 $r$ の等比数列
【階差型】$a_{n+1}=a_n+$ $(n\text{ の式})$
数列 $\left\{(n\text{ の式})\right\}$ が階差数列
これら3パターンは,初項さえ分かっていれば,公式を用いて瞬時に一般項が求められます。
上から順番に,等差数列,等比数列,階差数列を表しているのは分かるでしょうか。
具体的に見ていきます。
【等差型】 $a_{n+1}=a_n+d$
「$d$ を足したら次の項」と読みとれるので公差 $d$ の等差数列を表しています。よって,等差数列の一般項の公式を使うだけ。
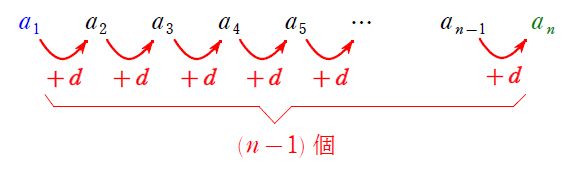
$a_n=a_1+(n-1)d$
【等比型】$a_{n+1}=ra_n$
「$r$ をかけたら次の項」と読みとれるので公比 $r$ の等比数列を表しています。よって,等比数列の一般項の公式を使うだけ。
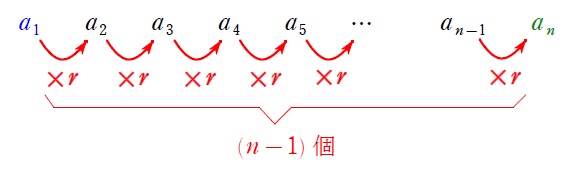
$a_n=a_1\cdot r^{n-1}$
【階差型】$a_{n+1}=a_n+(n\text{ の式})$
$(nの式)$ を $b_n$ とおけば,$b_n=a_{n+1}-a_n$ となって,$\left\{b_n\right\}$ は $\left\{a_n\right\}$ の階差数列。よって,階差数列から一般項を求める公式により $a_n$ が求まる。

$n≧2\text{ のとき} a_n=a_1+\displaystyle\sum_{k=1}^{n-1}{b_k}$
問題と解答(等差型,等比型,階差型)
【等差型】【等比型】【階差型】の3パターンについて,問題を見てみましょう。これらは,見てすぐ解けるようになるのは当然として,式の形で覚えるだけでなく,意味を理解して解けるようにしましょう。
問題(等差型,等比型,階差型)
(1) $a_1=1$,$a_{n+1}=a_n+3$
(2) $a_1=4$,$a_{n+1}=2a_n$
(3) $a_1=0$,$a_{n+1}=a_n+4n^3$
解答(等差型,等比型,階差型)
(1) $a_1=1$,$a_{n+1}=a_n$ $+$ $3$ 【等差型】
( $3$ 足したら次の項→等差数列)
初項 $1$,公差 $3$ の等差数列より
$a_n=1+(n-1)\times3$
∴ $a_n=3n-2$ (答)
(2) $a_1=4$,$a_{n+1}=$ $2$$a_n$ 【等比型】
( $2$ かけたら次の項→等比数列)
初項 $4$,公比 $2$ の等比数列より
$a_n=4\cdot2^{n-1}$
∴ $a_n=2^{n+1}$ (答)
(3) $a_1=0$,$a_{n+1}=a_n$ $+$ $4n^3$ 【階差型】
( 階差が $n$ の式→階差数列から一般項)
数列 $\left\{4n^3\right\}$ が階差数列より
$n≧2$ のとき
$a_n=$ $a_1$ $+$ $\displaystyle\sum_{k=1}^{n-1}{4k^3}$
$=0+4\times \left\{\displaystyle\frac{1}{2}(n-1)n\right\}^2$
$=n^{2}(n-1)^2$
これは,$n=1$ のときも成り立つ。
よって $a_n=n^{2}(n-1)^2$ (答)
漸化式における最重要パターン
【特殊解型】 $a_{n+1}=pa_n+q$
この型は,漸化式の中でも出題頻度が非常に高く,最も重要です。理解して素早く一般項を求められるようにして欲しいパターンです。
【特殊解型】$a_{n+1}=pa_n+q$ の考え方と例題
この形の漸化式は以下の手順で解きます。
① $a_{n+1}$ と $a_{n}$ を $\alpha$ と書き換えて
特性方程式 $\alpha=p\alpha+q$
の解 $\alpha$ を求める。(これを特殊解という)
② $a_{n+1}-\alpha=$ $p$$(a_n-\alpha)$ と変形
③ $\left\{a_n-\alpha\right\}$ は(公比 $p$ の)等比数列として求める
① $\alpha=2\alpha-3$ を解くと $\alpha=3$
② 漸化式は
$a_{n+1}-3=2(a_n-3)$ 【等比型】と変形できる
③ 数列 $\left\{a_n-3\right\}$ は
初項 $a_1-3=8-3=5$,
公比 $2$ の等比数列より,
$\left\{a_n-3\right\}$ の一般項は
$a_n-3$ $=$ $5$ $\cdot$ $2^{n-1}$
よって
$a_n=5\cdot2^{n-1}+3$ (答)
①と②は機械的に行えば良いでしょう。ちなみに,①は答案に書かないように。③については式を理解して解き進める必要があります。ここも機械的に解いてしまう人がいますが,意味も分からず解いていると,応用問題で行き詰まります。以下のことをしっかり理解しよう。
$a_{n+1}-3=2(a_n-3)$
この式を見て $\left\{a_n-3\right\}$ が等比数列と読み取れるでしょうか。$a_n-3$ をひとかたまりと見れば,

と読み取って,数列 $\left\{a_n-3\right\}$ が公比 $2$ の等比数列ということができます。
初項は $n=1$ としたものなので,$a_1-3$ である。 ($-3$ を忘れない)
これにより,一般項が求まりますが,今考えている数列は $\left\{a_n-3\right\}$ です。よって,$a_n$ ではなく$a_n-3$ が求まるので,忘れずに $-3$ を移項する。
教科書の場合 $a_n-3=b_n$ とおいて,
$b_{n+1}=2b_n$
と書いてから,等比数列として求める場合が多いが,受験で数学を使う人は $b_n$ とおかずに解いて欲しい。
理解のため,次のような例も見てみましょう。
$=3(a_n+2n+4)$
という条件式が与えられたとき,$a_n+2n+4$ をひとかたまりと見れば,

数列 $\left\{a_n+2n+4\right\}$ が公比 $3$ の等比数列と読み取れる。(読み取れますか?)
この数列の初項は $(n=1\text{ を代入して})$ $ a_1+2\cdot1+4$ である。
問題と解答(特殊解型)
問題(特殊解型)
$a_1=3$,$a_{n+1}=3a_n+4$
解答(特殊解型)
$a_{n+1}=3a_n+4$
漸化式を変形して
$a_{n+1}+2=$ $3$$(a_n+2)$ 【等比型】
[$\alpha=3\alpha+4$ を解くと $\alpha=-2$]
よって,$\left\{a_n+2\right\}$ は,
初項 $a_1+2=5$,公比 $3$ の等比数列より,
$a_n+2$ $=$ $5$ $\cdot$ $3^{n-1}$
したがって,$a_n=5\cdot3^{n-1}-2$ (答)
補足説明(特殊解型)
$\alpha=3\alpha+4$ を解くと $\alpha=-2$
[ここは答案に書かない]
この $\alpha$ の値を用いて
$a_{n+1}+2=3(a_n+2)$ 【等比型】
と変形できる。
符号に注意すること。
$a_{n+1}-(-2)=3\left\{a_n-(-2)\right\}$
変形さえできれば
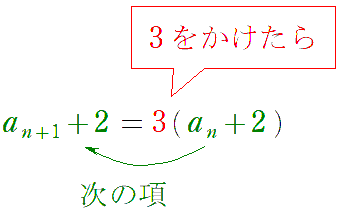
と読み取ればよい。
最終的に $a_n=5\cdot3^{n-1}-2$ と求まるが,念のため検算しておく。
$a_1=5\cdot3^0-2=5-2=3$ より
問題文の $a_1=3$ と一致する。
$a_2=5\cdot3^1-2=13$
もとの漸化式の両辺に $n=1$ を代入して
$a_2=3a_1+4=3\cdot3+4=13$
よって,$a_2$ も一致する。
漸化式において,このパターンが解けるかどうかで大きく差がつく。典型パターンの多くは,この型に帰着されるためである。この型が解けないことには何も始まらないので,しっかり理解して解けるようにして欲しい!
漸化式土台4パターンはこれで「解ける!」
【等差型】 $a_{n+1}=a_n+d$
【等比型】$a_{n+1}=ra_n$
【階差型】$a_{n+1}=a_n+(n\text{ の式})$
【特殊解型】$a_{n+1}=pa_n+q$

