$2$ 次関数の最大値,最小値は
平方完成!
グラフを描いて
軸からの距離に着目!
2次関数の最大値,最小値の考え方
2次関数の最大値,最小値を求める問題は,とにかく平方完成してグラフを描くことが基本です。グラフを描くと言っても,丁寧にすべて描く必要はありません。以下の3つが分かるように描けば問題ありません。
2次関数の最大値,最小値を求めるときの手順
どこからどう見ても2次関数なので平方完成する。
$$y=(x-2)^{2}-1$$
グラフを描く。今回は $x^{2}$ の係数が正なので下に凸です。また,今回のように定義域に制限がある場合は点線で描いておこう。$x$ 軸と $y$ 軸は不要なので描かない。

軸 $x=2$ を描く。
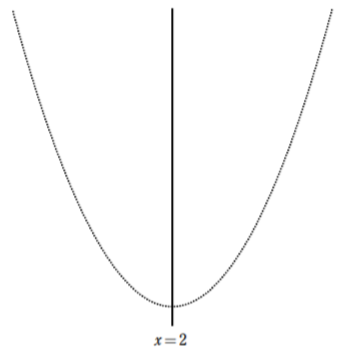
定義域内のグラフを実線で描く。このとき,定義域の両端のうち,どちらが軸から遠いのかを意識して描こう。今回は軸が $x=2$ なので $1$ と $4$ では $4$(右端) の方が遠い。
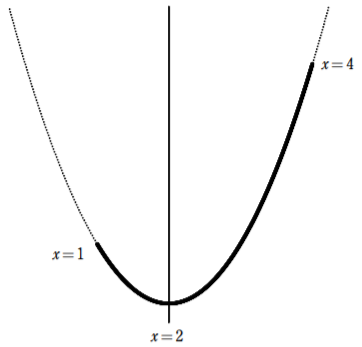
最も上にある点が最大,最も下にある点が最小。グラフを見ながら最大値と最小値を求める。
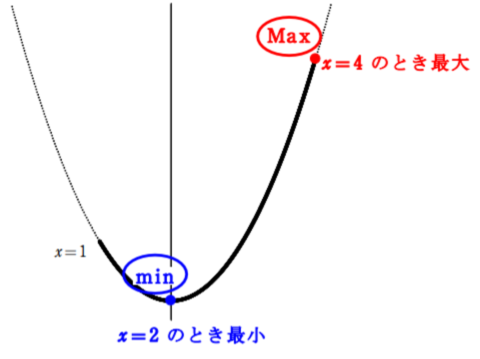
$$\begin{cases} x=4\text{ のとき 最大値 }3\\ x=2\text{ のとき最小値 }-1\end{cases}$$
2次関数の最大値,最小値を求める問題
それでは,あと3問ほど解いてみて感覚を掴みましょう。
問題
(1) $y=-2x^2-8x-2$
$(-4<x≦-1)$
(2) $y=\sqrt{x^2-2x}$ $(3≦x≦5)$
(3) $y=\cos^2{x}-\cos{x}+1$
$(0°≦x≦180°)$
(1) の解答
2次関数だからという理由は、必ず意識してくださいね。
<解答>
$y=-2x^{2}-8x-2$
$=-2(x^{2}+4x)-2$
$=-2\left\{ (x+2)^{2}-4\right\}-2$
$=-2(x+2)^{2}+6$ [平方完成]
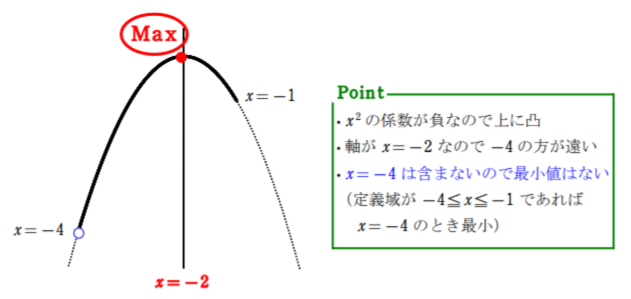
よって
$\begin{cases} x=-2\text{ のとき 最大値 }6\\ \text{最小値はない}\end{cases}$ (答)
(2) の解答
$y=\sqrt{ x^{2}-2x }$ $(3≦x≦5)$
<解答>
$f(x)=x^{2}-2x$ $(3≦x≦5)$ とおく。
$f(x)=(x-1)^{2}-1$ [平方完成]
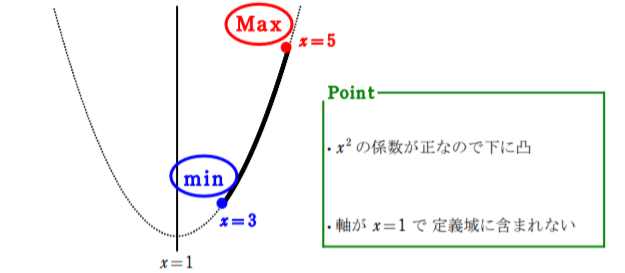
よって,$f(x)$ は
$\begin{cases} x=5\text{ のとき 最大値 }15\\ x=3 \text{ のとき 最小値 }3\end{cases}$
したがって,$y$ は
$\begin{cases} x=5\text{ のとき 最大値} \sqrt{ 15 }\\ x=3\text{ のとき 最小値} \sqrt{ 3 }\end{cases}$ (答)
(3) の解答
$y=\sin^{2} x-\sin x+1$ $(0°≦x≦180°)$
<解答>
$\sin x=t$ とおくと
$0°≦x≦180°$ より $0≦t≦1$
このとき
$y=t^{2}-t+1$ [$t$ の2次関数]
$=\left(t-\displaystyle\frac{1}{2}\right)^{2}+\displaystyle\frac{3}{4}$ $(0≦t≦1)$ [平方完成]
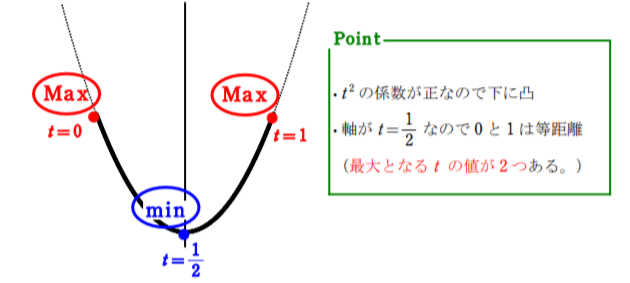
よって $\begin{cases} t=0,1\text{ のとき 最大値 }1\\ t=\displaystyle\frac{1}{2}\text{ のとき最小値 } \displaystyle\frac{1}{2}\end{cases}$
ここで,
$t=0$ のとき $\sin x=0$ より $x=0°, 180°$
$t=1$ のとき $\sin x=1$ より $x=90°$
$t=\displaystyle\frac{1}{2}$ のとき $\sin x=\displaystyle\frac{1}{2}$ より $x=30°, 150°$
よって,
$\begin{cases} x=0°, 90°, 180°\text{ のとき 最大値 }1\\ x=30°, 150°\text{ のとき最小値 } \displaystyle\frac{1}{2}\end{cases}$ (答)
2次関数の最大値,最小値がこれで「解ける」へ!

