等差数列は「一般項」と「和」を求められるようになることが目標です。ここで身に付けた内容は,この先の内容で出てくる「$\sum$ (シグマ)の計算」や「漸化式」でも必要になります。数列の土台となる部分なので,穴がないようにしておく必要があります。公式さえ覚えてしまえば解けるという認識で軽視されがちですが,公式の覚え方を誤ると,少し変化があるだけでたちまち解けなくなるので注意が必要です。基本は「文字ではなく言葉で覚える」ですが,細かい話はそれぞれの項目で伝えていきます。
等差数列の意味や公式は知ってるよって人は問題までジャンプしてしまって大丈夫です。
等差数列とは(知らない人向け)
まず,等差数列とは何でしょうか。
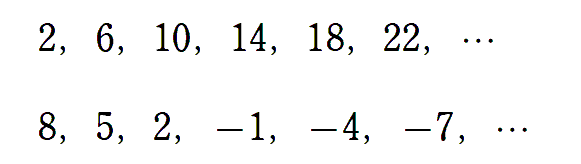
上の $2$ つの数列はある規則で並んでいるけど,分かるかな?
そうですね。同じ数ずつ増えたり,減ったりしていますね。
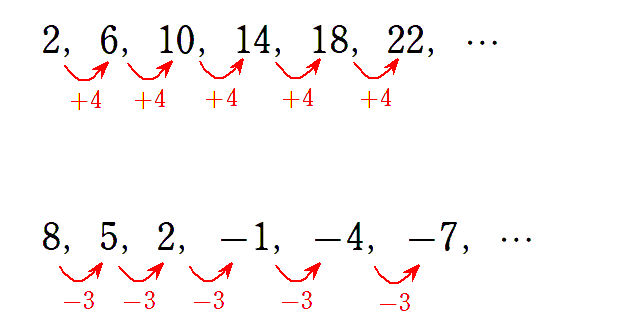
このように同じ数ずつ増えている(減っている)数列を等差数列と言います。
ちなみに,この増えている(減っている)数のことを公差と言います。

等差数列の本来の意味(定義)は「隣り合う項の差が等しい数列」です。
差が等しい数列で「等差数列」ですね。言っていることは同じなので,理解しやすい方で理解しておきましょう。
等差数列の一般項の公式
次の等差数列について考えてみます。
$2$,$5$,$8$,$11$,$\cdots$
問題です。
これは簡単ですね。$3$ ずつ足していけばいいので,
$2$,$5$,$8$,$11$,$14$,$17$,$20$,$23$
$23$ ですね。では,次の問題はどうしますか?
$1001$ 個書き出せば分かるけど,さすがにそんなことをする元気はないと思います。
ここで,規則をうまく使って求めてみましょう。
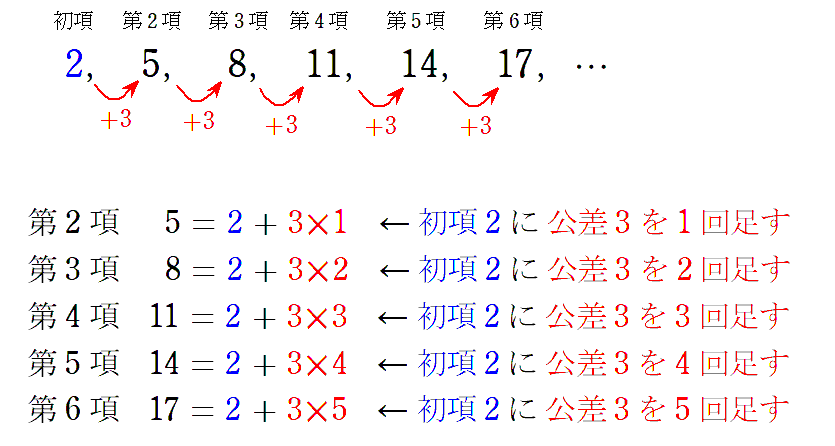
公差を何回足しているかに注目してみると,何か規則がありそうです。
では,第 $1001$ 項は初項 $2$ に公差 $3$ を何回足したものでしょうか。
もう分かりますね。$1000$ 回足したものなので
$$\left(\text{第 }1001\text{ 項}\right)=2+1000\times3=3002$$
規則を使えば,第何項であっても求められますね。
第 $8$ 項は $2+$ $7\times3$ $=23$
第 $100$ 項は $2+$ $99\times3$ $=299$
第 $321$ 項は $2+$ $320\times3$ $=962$
第 $n$ 項は $2+$ $(n-1)\times3$ $=3n-1$
公差を $1$ 個少ない個数だけ足しているという認識が重要です。
次が,一般項 (第 $n$ 項) の公式です。
$$a_n=a+(n-1)d$$ $$\left[\text{初項 }a\text{ に公差 }d\text{ を }(n-1)\text{ 回足す}\right]$$
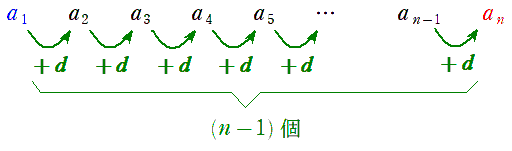
式の丸暗記ではなく,初項 $a$ に公差 $d$ を $1$ 個少ない個数足しているという理解をしておきましょう。
また,一般項を求めるために必要なものは「初項」と「公差」の $2$ つという意識を持っておきましょう。
等差数列の和の公式
では次の問題です。
やはり,規則をうまく使って求めてみましょう。
$S$ を次のように並べて書いてみます。
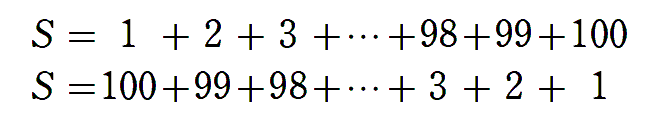
上と下を足してみると

よって,$2S=100×101$
これは $S$ を $2$ つ合わせたものなので $2$ で割って
$S=\displaystyle\frac{1}{2}\times100\times101=5050$
無事,求まりました。
ここで,意識しておいて欲しいのは,
$100$ は項数 ($1$ から $100$ なので $100$ 個)
$101$ は初項(最初の数) $1$ と末項(最後の数) $100$ の和
であることです。
これを利用して $1$ つ前の問題を考えてみると,
$1$$+2+3+\cdots+$$10$
・初項(最初の数)は $1$
・末項(最後の数)は $10$
・項数は $10$
だから,和は
$S=\displaystyle\frac{1}{2}\times$$10$$\times ($$1$$+$$10$$)=55$
となって,電卓の結果と一致しましたね!
次が等差数列の和の公式です。
$$S=\displaystyle\frac{1}{2}n(a+l)$$ $$\left[\displaystyle\frac{1}{2}\times (\text{項数})\times (\text{初項}+\text{末項})\right]$$
等差数列の和は公式を言葉で覚えて「初項」「末項」「項数」から求めている意識が重要です。
ちなみに,教科書には $\displaystyle\frac{1}{2}n\left\{2a+(n-1)d\right\}$ という公式があるけど,使うことはないので覚えなくていいです。むしろ,考え方に一貫性がなくなるので覚えない方がいいです。なぜ成り立つかを考えることは良いことなので,ぜひ考えてみてください。
等差数列の一般項と和に関する問題と解き方
実際に問題を解いてみましょう。解説では,どのように考えているかまで含めて説明します。この「考え方」を理解して初めて「解ける」ようになります。授業のように質問を入れながら進めるので,考えながら読み進めてみてください。実際に紙に書ける状況なら,授業を受けているように手を動かしながら進めるとより理解できます。解説のあとに,必要なことだけを書いた答案があります。自力で答案部分を書けるようになることが目標です。
問題
等差数列 $\left\{a_n\right\}$ が,$a_{11}=48$, $a_{20}=21$ を満たすとする。
(1) 数列 $\left\{a_n\right\}$ の一般項を求めよ。
(2) 数列 $\left\{a_n\right\}$ の第 $11$ 項から第 $20$ 項までの和 $S$ を求めよ。
解説(授業)
(1) 等差数列の一般項を求める問題ですね。
等差数列の一般項を求めるために必要なものは何でしょうか。
ちゃんと言えますか?
はい「初項」と「公差」でしたね。
つまり「等差数列の一般項を求めよ」は「初項と公差を求めよ」と言われているのと同じです。
よって,初項を $a$,公差を $d$ とおきます。数学において,求めたいものを文字でおくのは基本ですね。
次に,どうやって $a$ と $d$ を求めるかですが,$a$ と $d$ の関係式を何個用意すればこれらが求められるか言えますか?
答えは $2$ 個です。
あまり意識していない人も多いと思いますが,文字の個数と同じ個数の式を用意するというのは,数学の最重要事項の $1$ つです。意識してなかったという人は,意識する練習を普段からしておきましょう。
では,どうやって $2$ 個の式を作るかですが,$a_{11}=48$,$a_{20}=21$ に着目すれば良いというのは気づきますよね。
$a_{11}$ (第 $11$ 項) は初項 $a$ に公差 $d$ を $10$ 回足したものなので
$a_{11}=a+10d$
$a_{20}$ (第 $20$ 項) は初項 $a$ に公差 $d$ を $19$ 回足したものなので
$a_{20}=a+19d$
これと $a_{11}=48$,$a_{20}=21$ から次のような連立方程式が立てられますね。
$\begin{cases}a+10d=48 \enspace\cdots\text{①}\\a+19d=21\enspace\cdots\text{②}\ \end{cases}$
解きます。
$\text{②}-\text{①}$ より $9d=-27$
よって $d=-3$
①に代入して $a+10\times(-3)=48$
よって $a=78$
初項 $78$,公差 $-3$ であるから,
$a_{n}$ $=$ $78$ $+$ $(n-1)\times(-3)$
[$a_n$ は初項 $78$ に公差 $-3$ を $(n-1)$ 回足したもの]
よって,$a_n=-3n+81$ (答)
検算もしておきましょう。
$n=11$ を代入して $a_{11}=-3\times11+81=48$
$n=20$ を代入して $a_{20}=-3\times20+81=21$
大丈夫そうですね。
数列分野は $n=1$ や問題で与えられている値などで検算が可能です。
解ける問題で失点しないように,検算する癖はつけておきましょう。
(2) 等差数列の和の問題ですね。
等差数列の和を求めるために必要なものは何でしょうか。
「初項」「末項」「項数」の $3$ つでしたね。
それぞれいくつになるか考えてみてください。
数列 $a_{11}$,$a_{12}$,$a_{13}$,…,$a_{20}$
の和なので,
初項 $a_{11}=48$,末項 $a_{20}=21$ です。
項数は $10$ ですが,ここで間違える人が多いので気を付けましょう。
$11~20$ だから $20-11=9$ より 項数 $9$ と間違える人が多いです。
$20-11$ としてしまうと,$a_{11}$ を除いてしまっているので。$1$ 足したものが項数となります。
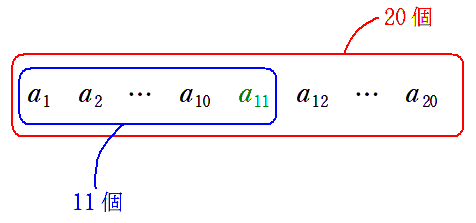
× $\text{(項数)}$ $=$ $20$ $-$ $11$ $=9$ (間違い!)
○ $\text{(項数)}$ $=$ $20$ $-$ $11$ $+1$ $=10$
[(後)$-$(前)$+1$ と覚えておこう!]
あとは,等差数列の和の公式
$\text{(等差の和)}$
$=\displaystyle\frac{1}{2}\times \text{(項数)}\times \text{(初項+末項)}$
で求めるだけですね。
初項 $48$,末項 $21$,項数 $10$ より
$S=\displaystyle\frac{1}{2}\times$$10$$\times ($$48$$+$$21$$)=345$ (答)
整理の意味も込めて,実際の答案を確認してみてください。
答案
(1) 初項 $a$,公差 $d$ とする
$a_{11}=48$,$a_{20}=21$ より
$\begin{cases}a+10d=48\\a+19d=21 \end{cases}$
これを解いて $a=78$,$d=-3$
よって,一般項は
$a_n=78+(n-1)\times(-3)$
∴ $a_n=-3n+81$ (答)
(2) 求める和は
$a_{11}$ $+a_{12}+\cdots+$ $a_{20}$
初項 $a_{11}=48$,末項 $a_{20}=21$,項数 $10$ の等差数列の和より,
$\displaystyle\frac{1}{2}\times10\times(48+21)$ $=345$ (答)
等差数列がこれで「解ける!」
$=\displaystyle\frac{1}{2}\times \text{(項数)}\times \text{(初項+末項)}$

