微分による最大値，最小値の求め方

基本例題（微分による最大最小）

関数 $f(x)=2x^{3}-3x^{2}-12x+1$ $(-2≦x≦4)$ の最大値と最小値を求めよ。

例題の解答

$f'(x)=6x^{2}-6x-12$
　　　$=6(x^{2}-x-2)$
　　　$=6(x+1)(x-2)$
　よって，$f(x)$ の増減表は

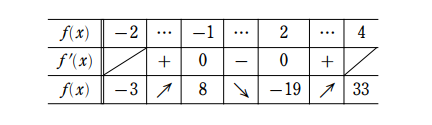
増減表より
$\begin{cases}x=4\text{ のとき 最大値 }33\\x=2\text{ のとき 最小値 }-19 \end{cases}$　(答)

例題の解説

　２次関数ではなく，$○+\displaystyle\frac{\text{定数}}{○}$ とすることもできないので，微分して，増減表から最大値，最小値を求める。

　今回の問題は教科書にあるような素直な問題だが，$f'(x)$ の扱いについて触れておく。$f'(x)$ の符号部分を「具体的に $x$ の値を代入して調べている」という人は要注意！

　$f(x)=2x^{3}-3x^{2}-12x+1$ を微分して因数分解すると

　$f'(x)=6$$(x+1)(x-2)$

となり，符号が変化する部分を抜き出し，$y=(x+1)(x-2)$ のグラフを描く。

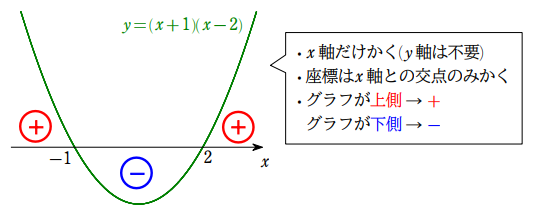
　グラフは「形」と「$x$ 軸との共有点」に着目して描こう。今回は 「２次関数だから放物線」「$(x+1)(x-2)=0$ を解いて， $x$ 軸との共有点は $x=-1, 2$」

　このグラフから，増減表の $f'(x)$ の符号を埋める。代入して調べた方がラクと思う人もいるかもしれないが，複雑な値を代入しなくてはならなかったり，そもそも代入する値が分からなかったりする場合がある（数Ⅲ）。

　増減表を書いたら，増減表を見て最大値と最小値を答えるだけ。

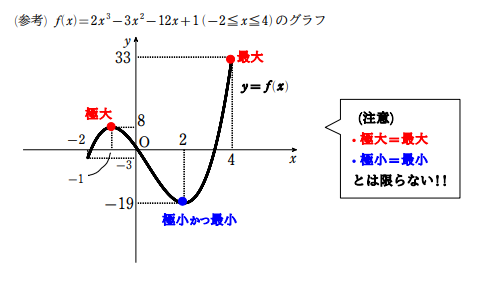
問題(微分による最大値，最小値)

(1) の解答

$f(x)=x^{4}-2x^{3}+x^{2}+1$ $(0<x≦2)$

$f'(x)=4x^{3}-6x^{2}+2x$
　　　$=2x(2x^{2}-3x+1)$
　　　$=2x(2x-1)(x-1)$
　よって，$f(x)$ の増減表は

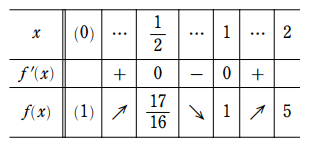
増減表より

$\begin{cases}x=2\text{ のとき 最大値 }5\\x=1\text{ のとき 最小値 }1 \end{cases}$　(答)

(1) の解説・考え方の根拠

　微分して，増減表から求めるという方針は立つだろう。

　$f'(x)=2x$$(2x-1)(x-1)$

　$x>0$ に注意すれば $f'(x)$ の符号を決めるのは $(2x-1)(x-1)$ の部分。

　$y=(2x-1)(x-1)$ のグラフを描くと

このグラフから，増減表の $f'(x)$ の符号を埋める。（代入して調べようとすると，$\displaystyle\frac{1}{2}$ と $1$ の間の値を代入することになるので面倒。）

　増減表さえかければ，最大値と最小値はすぐ求まる。$x=0$ は定義域に入っていないため，「$x=0, 1\text{ のとき 最小値 }1$」と書かないように注意。

(2) の解答

$f(x)=x^{2}-2x-4\log_{}{(x^{2}+1)}$

$f'(x)=2x-2-4\cdot\displaystyle\frac{2x}{x^{2}+1}$

$=\displaystyle\frac{2x(x^{2}+1)}{x^{2}+1}+\displaystyle\frac{-2(x^{2}+1)}{x^{2}+1}+\displaystyle\frac{-8x}{x^{2}+1}$

$=\displaystyle\frac{2x^{3}-2x^{2}-6x-2}{x^{2}+1}$

$=\displaystyle\frac{2(x^{3}-x^{2}-3x-1)}{x^{2}+1}$

$=\displaystyle\frac{2(x+1)(x^{2}-2x-1)}{x^{2}+1}$

よって，$f'(x)=0\text{ のとき }x=-1，1\pm\sqrt{2}$ より $f(x)$ の増減表は

ここで，
$f(-1)=3-4\log_{}{2}$
$f(1+\sqrt{2})=1-4\log_{}{(4+2\sqrt{2})}$

よって，
$f(-1)$ $>$ $f(1+\sqrt{2})$ であるから，

$x=1+\sqrt{2}$ のとき
最小値 $1-4\log_{}{(4+2\sqrt{2})}$　(答)

(2) の解説・考え方の根拠

　これも微分して，増減表から求めるという方針は立つだろう。

　まず，$f'(x)=\displaystyle\frac{2(x+1)(x^{2}-2x-1)}{x^{2}+1}$ まで計算できるだろうか。

$f(x)=x^2-2x-4\log{(x^2+1)}$

微分して

$f'(x)=2x-2-4\cdot\displaystyle\frac{2x}{x^{2}+1}$

$\left[\left\{\log_{}{f(x)}\right\}’=\displaystyle\frac{f'(x)}{f(x)}\right]$

　分数が混じっている場合は通分して 1 つにまとめるのが鉄則。通分して計算すると，

$$f'(x)=\displaystyle\frac{2x^{3}-2x^{2}-6x-2}{x^{2}+1}$$

　$f'(x)$ の符号，$f'(x)=0$ のときの $x$ の値が必要なので，分子を因数分解する。まず，共通因数の $2$ でくくり

$$f'(x)=\displaystyle\frac{2(x^{3}-x^{2}-3x-1)}{x^{2}+1}$$

　$x^{3}-x^{2}-3x-1$ の部分は $3$ 次式なので，因数定理を用いて因数分解する。$x=-1$ を代入すると $0$ になるので，$(x+1)$ を因数にもつ。これより，

$$f'(x)=\displaystyle\frac{2(x+1)(x^{2}-2x-1)}{x^{2}+1}$$

　計算を終えたら，符号に注目する。$x^{2}+1>0$ であるから $f'(x)$ の符号を決めるのは $(x+1)(x^{2}-2x-1)$ の部分。$y=(x+1)(x^{2}-2x-1)$ のグラフを描くと

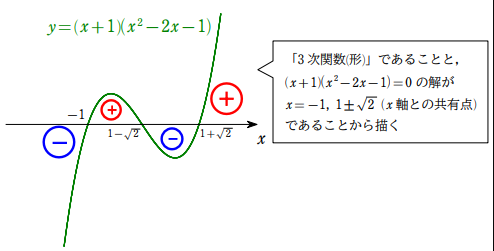
　このグラフから，増減表の $f'(x)$ の符号を埋め，増減表を作成する。

　さて，今回求めるのは最小値であるが，$f(-1)$，$f(1-\sqrt{2})$，$f(1+\sqrt{2})$ のうち，最小値となり得るものを考える。何も考えず，すべて計算してはならない。増減表から $f(1-\sqrt{2})$ が最小値となることは絶対にない（増加したあとの点であるため）。$f(-1)$ と $f(1+\sqrt{2})$ の大小関係は増減からは分からないので，実際に計算して比較する。小さい方が最小値。

$f(-1)=3-4\log_{}{2}$
$f(1+\sqrt{2})=1-4\log_{}{(4+2\sqrt{2})}$

 $f(-1)$ $-$ $f(1+\sqrt{2})$

　$=$ $3-4\log_{}{2}$$-$$\left\{1-4\log_{}{(4+2\sqrt{2})}\right\}$

　$=2-4\left\{\log_{}{2}-\log_{}{(4+2\sqrt{2})}\right\}$

　$=2+4\left\{\log_{}{(4+2\sqrt{2})}-\log_{}{2}\right\}$

　$=2+4\log_{}{(2+\sqrt{2})}$

$\left[\log_{a}{M}-\log_{a}{N}=\log_{a}{\displaystyle\frac{M}{N}}\right]$

　　$>0$

$\left[\log_{}{(2+\sqrt{2})}>\log_{}{1}=0\text{ より}\right]$

よって　$f(-1)$ $-$ $f(1+\sqrt{2})$ $>$ $0$
すなわち　$f(-1)$ $>$ $f(1+\sqrt{2})$
ゆえに　最小値は $f(1+\sqrt{2})$

これで「解ける」へ！