三角関数の合成による最大値，最小値の求め方

三角関数の合成（公式）

合成の手順

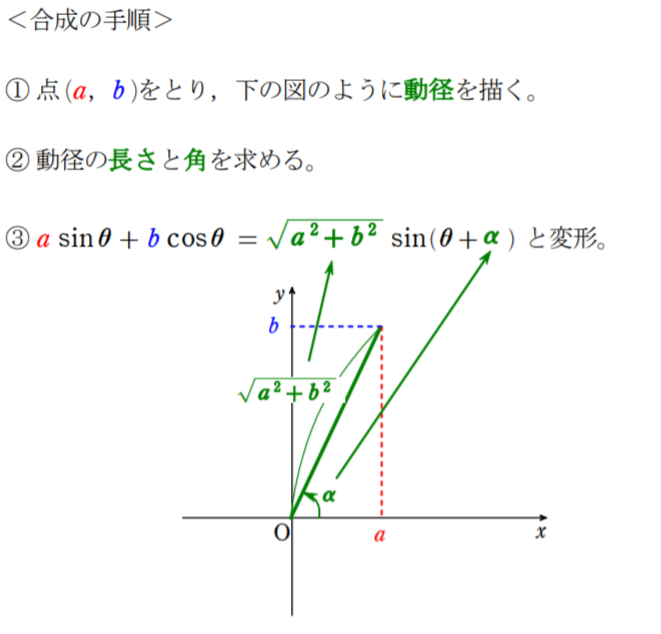
問題(合成による最大値，最小値)

(1) の解答

$\sin x+\sqrt{3}\cos x$ $(0≦x≦\pi)$

$\sin x+\sqrt{3}\cos x=2\sin \left(x+\displaystyle\frac{\pi}{3}\right)$　[合成]

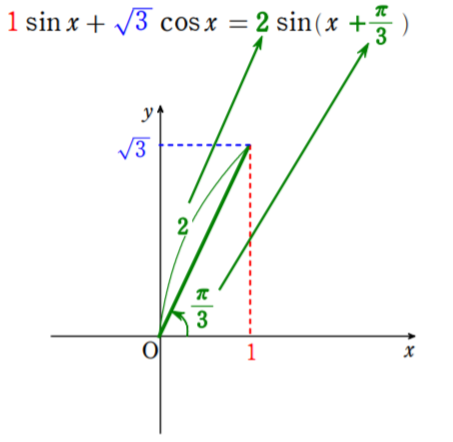
(1) の解説・考え方の根拠

$a\sin x+b\cos x$ はまず合成。図を描きながら，素早く正確に合成できるようにしよう。

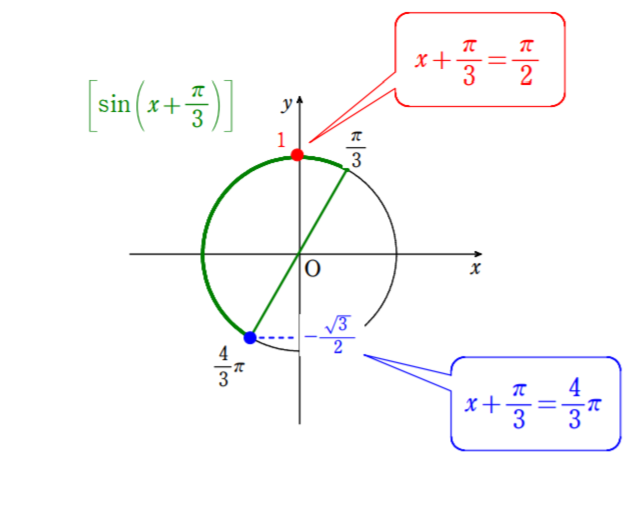
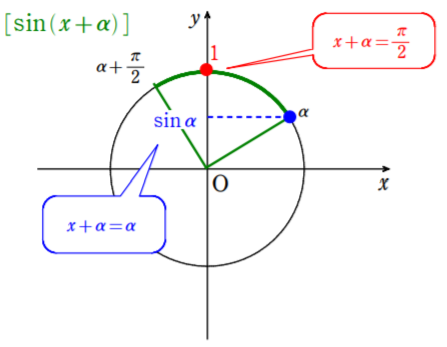
　合成をすれば $\sin \left(x+\displaystyle\frac{\pi}{3}\right)$ の値の範囲を求める問題に帰着する。角の範囲に注意して，解答のように単位円を図示して求める。

(2) の解答

$4\sin{x}+3\cos{x}$ $\left(0≦x≦\displaystyle\frac{\pi}{2}\right)$

$4\sin x+3\cos x=5\sin (x+\alpha)$　[合成]

ただし，$\cos\alpha=\displaystyle\frac{4}{5}，\sin\alpha=\displaystyle\frac{3}{5}$

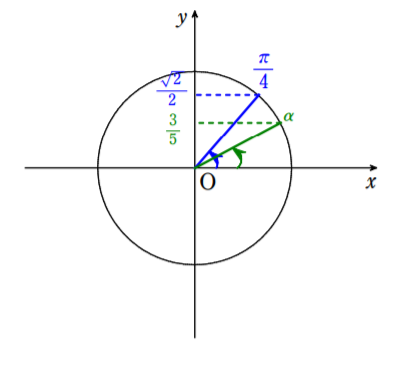
(2) の解説・考え方の根拠

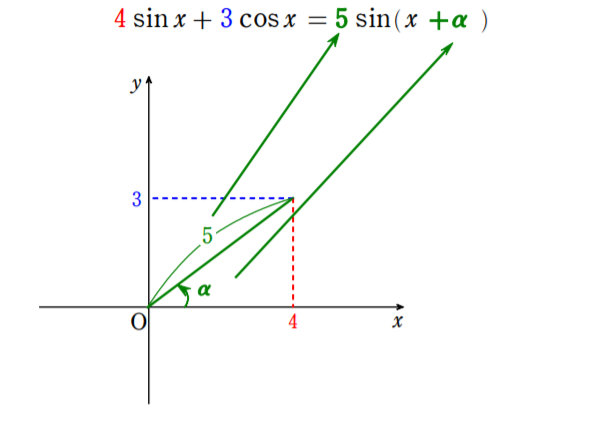
　合成するが，有名角でない角が現れる。分からないので角を $\alpha$ としておき，$\cos\alpha，\sin\alpha$ の値を記述しておく。角が分からなくても $\cos\alpha，\sin\alpha$ の値を用いることにより問題が解けるパターンは多いので，「分からない角は $\alpha$ とおいて $\cos\alpha，\sin\alpha$ の値を用いる」を知識として入れておこう。

　最大値，最小値を求める流れは (1) と同じであるが，$\alpha$ が分からないため問題が生じる。
$\alpha ≦x+\alpha ≦\alpha+\displaystyle\frac{\pi}{2}$ における $\sin (x+\alpha)$ の範囲を調べるが，$\alpha$ の動径のかき方によって，最小値が $\sin \alpha$ だったり，$\sin \left(\alpha+\displaystyle\frac{\pi}{2}\right)$ だったりする。（下の図参照）

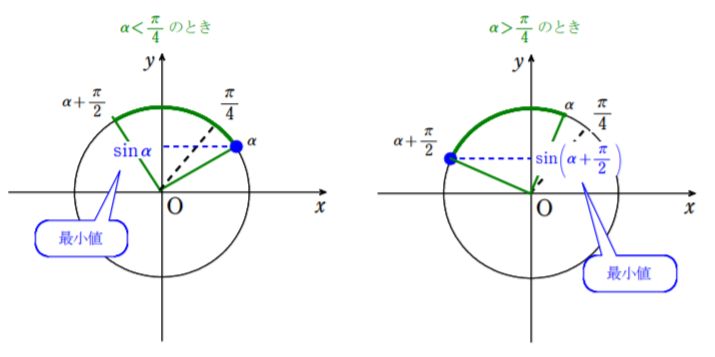
　結局，$\alpha$ と $\displaystyle\frac{\pi}{4}$ の大小関係を調べることになる。しかし，$\alpha$ そのままで比較することはできないので，サイン(またはコサイン)の値で比較する。

$\sin\alpha=\displaystyle\frac{3}{5}=\displaystyle\frac{6}{10}=\displaystyle\frac{\sqrt{36}}{10}$

$\sin \displaystyle\frac{\pi}{4}=\displaystyle\frac{\sqrt{2}}{2}=\displaystyle\frac{5\sqrt{2}}{10}=\displaystyle\frac{\sqrt{50}}{10}$
(大小比較ができるように分母を $10$ にそろえた)

よって

　$\sin\alpha$ $<$ $\sin \displaystyle\frac{\pi}{4}$

[$\alpha$ の方が $y$ 座標が小さい（下側)]

すなわち

$0<$ $\alpha$$<$ $\displaystyle\frac{\pi}{4}$

を得て，さっきの図において，左側の図の位置関係であることが判明する。

$x+\alpha=\displaystyle\frac{\pi}{2}$ のとき最大
$x+\alpha=\alpha$ のとき最小
となることが分かる。

これで「解ける」へ！