【入試問題】sinθ+cosθ=tとおくパターンと，直線のなす角に関する最大値，最小値

問題（山口東京理科大）

(1) の解答

$t=\sin \theta+\cos \theta$ $=\sqrt{2}\sin \left(\theta+\displaystyle\frac{\pi}{4}\right)$　[合成]

(1) の解説・考え方の根拠

$t$ の範囲は $a\sin \theta+b\cos \theta$ の形を見て合成してしまえばすぐ求まる。

「とり得る値の範囲」は，結局のところ最大値と最小値を聞かれているだけである。合成による最大値，最小値の求め方については以下の記事を参照。

(2) の解答

$y=\sin 2\theta+1-\sin \theta-\cos \theta$
　$=2$ $\sin \theta\cos \theta$ $+1-($$\sin \theta+\cos \theta$$)$

ここで，
$t^2=(\sin \theta+\cos \theta)^2=1+2\sin \theta\cos \theta$

よって　$\sin \theta\cos \theta=\displaystyle\frac{t^2-1}{2}$

したがって，$y$ を $t$ で表すと

$y=2$ $\cdot$ $\displaystyle\frac{t^2-1}{2}$ $+1-$ $t$

整理して

$y=t^2-t$ $(-1≦t≦\sqrt{2})$
　[$t$ の２次関数]

$y=\left(t-\displaystyle\frac{t}{2}\right)^{2}-\displaystyle\frac{1}{4}$ $(-1≦t≦\sqrt{2})$
　[平方完成]

グラフより

$\begin{cases}(t=-1 のとき)\text{ 最大値 }2\\ (t=\frac{1}{2} のとき)\text{ 最小値 }-\displaystyle\frac{1}{4} \end{cases}$　(答)

(2) の解説・考え方の根拠

$y$ を $t$ の関数で表してみると，$t$ の２次関数となる。

２次関数であることから，瞬時に平方完成という選択ができるようにしたい。２次関数の最大値，最小値の求め方については，以下の記事を参照。

最大値，最小値を求める基本方針４パターンが頭に入っていれば悩むことなく解けるはず。土台となる考え方を頭に入れておく重要性を理解してほしい。

　この問題から得て欲しいことはもう１つある。(改) を入れているが，本来は (1) が存在せず，いきなり $y$ の最大値と最小値が聞かれている。つまり，$t=\sin \theta+\cos \theta$ の置き換えを自分で思いつく必要がある。実際，誘導がない場合はかなり多いので，どういうときにこの置き換えをするのか確認しておく。式を見てみよう

$$y=\sin 2\theta+1-\sin \theta-\cos \theta$$

　慣れてきた場合は，この式の時点で気づけるが、ひとまず $\sin 2\theta$ に $2$ 倍角の公式を用いて，角を $\theta$ に統一する。（三角関数において，角の部分をそろえるのは基本方針である）

$$y=2\sin \theta \cos \theta+1-\sin \theta-\cos \theta$$

　この式は $\sin \theta$ と $\cos \theta$ を入れ替えて書いても変わらないことに気付くだろうか。実際に入れ替えてみると

$$y=2\cos \theta \sin \theta+1-\cos \theta-\sin \theta$$

　となるが，確かに同じ式である。このような式を対称式という。（ 例えば $x^2+y^2$ や $x^3+xy+y^3$ は $x$ と $y$ の対称式である。）

　今回のような $\sin \theta$ と $\cos \theta$ の対称式は $t=\sin \theta+\cos \theta$ とおくということは知識として入れておく必要がある。当然，$t$ の範囲を求める必要が生じる。（合成）

これで「解ける」へ！①

問題（北海道大）

(1) の解答

図のように，
直線 AB と $x$ 軸の正の向きになす角を $\beta$，
直線 AC と $x$ 軸の正の向きになす角を $\gamma$

とすると，

直線 AB の傾きは $\displaystyle\frac{-2}{x+2}$　$[\displaystyle\frac{y\text{ の変化量}}{x\text{ の変化量}}]$

直線 AC の傾きは $\displaystyle\frac{-3}{x+3}$　$[\displaystyle\frac{y\text{ の変化量}}{x\text{ の変化量}}]$

より，

　$\tan \beta=\displaystyle\frac{-2}{x+2}$，$\tan \gamma=\displaystyle\frac{-3}{x+3}$

[$\tan $ $=$ 傾き]

よって，$\theta=\beta-\gamma$ より，

$\tan \theta=\tan (\beta-\gamma)$

　　　$=\displaystyle\frac{\tan \beta-\tan \gamma}{1+\tan \beta\tan \gamma}$ [$\tan$ の加法定理]

　　　$=\displaystyle\frac{\frac{-2}{x+2}-\frac{-3}{x+3}}{1+\frac{-2}{x+2}\cdot\frac{-3}{x+3}}$

　　　[$\tan \beta=\frac{-2}{x+2}$，$\tan \gamma=\frac{-3}{x+3}$]

　　　$=\displaystyle\frac{-2(x+3)+3(x+2)}{(x+2)(x+3)+6}$

　　　[分母分子に $(x+2)(x+3)$ かけた]

　　　$=\displaystyle\frac{x}{x^2+5x+12}$　(答)

(1) の解説・考え方の根拠

2 直線のなす角をテーマとした典型問題である。以下のことは知識として入れておきたい。
① 直線のなす角の問題は「$\tan = \text{傾き}$」を利用
②２直線のなす角は「$\tan$ の加法定理」を利用

① については，以下のことを基本事項として押さえておくこと。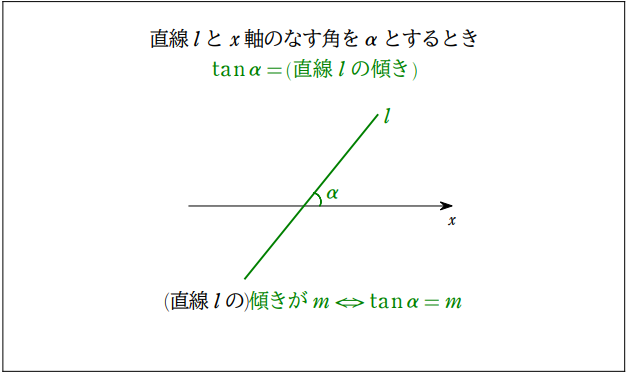

２直線のなす角に関する問題は，間違いなくこれらを利用する。
迷わず直線と$x$ 軸とのなす角を文字でおいて，解き進められるようにしたい。

(2) の解答

$\tan \theta=\displaystyle\frac{x}{x^2+5x+12}$　$(x>0)$ より

$\tan \theta=\displaystyle\frac{1}{x+\displaystyle\frac{12}{x}+5}$　[分母分子を $x$ で割った]

よって，$\tan \theta$ が最大となるのは，
$x+\displaystyle\frac{12}{x}$$+5$ が最小となるときである。

$x>0$，$\displaystyle\frac{12}{x}>0$ であるから，

$(\text{相加平均})≧(\text{相乗平均})$ より
$x+\displaystyle\frac{12}{x}≧2\sqrt{x\cdot\displaystyle\frac{12}{x}}$ $=4\sqrt{3}$

よって　$x+\displaystyle\frac{12}{x}+5≧4\sqrt{3}+5$

等号は $x=\displaystyle\frac{12}{x}$ すなわち $x=2\sqrt{3}$ のとき成り立つ。

以上より，$\tan \theta$ は

$x=2\sqrt{3}$ のとき，

最大値 $\displaystyle\frac{1}{4\sqrt{3}+5}=\displaystyle\frac{4\sqrt{3}-5}{23}$　(答)

(2) の解説・考え方の根拠

　$\displaystyle\frac{x}{x^2+5x+12}$　$(x>0)$ の最大値を求める問題である。しつこく言うが，最大値，最小値を求める基本方針４パターンが頭に入っていることが前提である。分母と分子を $x$ で割れば $x+\displaystyle\frac{12}{x}$ $(○+\displaystyle\frac{ \text{定数} }{ ○ }\text{ の形})$ が現れるため，$(\text{相加平均})≧(\text{相乗平均})$ を用いる。相加平均・相乗平均による最大値，最小値の求め方については，以下の記事を参照。

$\displaystyle\frac{x}{x^2+5x+12}$　$(x>0)$

この式の最大値を求めるとき，次のような思考で解ければよい。

最大値，最小値（１変数）の問題なので，まず基本方針４パターンを思い浮かべる。
[1] ２次関数は平方完成
[2] $○+\displaystyle\frac{ \text{定数} }{ ○ }$ は$(\text{相加平均})≧(\text{相乗平均})$
[3] $a\sin \theta+b\cos \theta$ なら合成
[4] 上記が無理なら微分

[1]と[3]は明らかに違うため除外。[2]と[4]が候補となる。[4]は他がすべて無理な場合に選択するので，[2]の方針で解けないか検討する。

つまり，「$○+\displaystyle\frac{ \text{定数} }{ ○ }$ の形を作ることができないだろうか」という視点で $\displaystyle\frac{x}{x^2+5x+12}$ を見るのである。

この視点で見ることによって，分母と分子を $x$ で割って $x+\displaystyle\frac{12}{x}$ に着目するという発想ができるのである。

ちなみに，理系(数学Ⅲ学習済み)であれば[4]の微分によって解くことも可能である。文系の場合は，[2]の方針で解くことに気付けなければ解くことができない。

これで「解ける」へ！②