【入試問題】$a^x+a^{-x}=t$ とおく最大値，最小値を求める問題

問題（早稲田大学）

解答

$2^x>0，2^{-x}>0$ であるから，$(相加平均)\text{≧}(相乗平均)$ より

$2^x+2^{-x}\text{≧}2\sqrt{2^x・2^{-x}}$$=2$

等号は $2^x=2^{-x}$ すなわち $x=0$ のとき成り立つ。

よって，$f(x)$ は $x=0$ のとき，最小値 $2$ (答_アイ)

$2^x+2^{-x}=t$ とおく。

$4^x+4^{-x}=(2^x+2^{-x})^{2}-2$

　[$x^2+y^2=(x+y)^2-2xy$]

よって，$4^x+4^{-x}=t^{2}-2$

$8^x+8^{-x}=(2^x+2^{-x})^{3}-3(3^x+3^{-x})$

　[$x^3+y^3=(x+y)^3-3xy(x+y)$]

よって，$8^x+8^{-x}=t^{3}-3t$

したがって，

$g(x)=$$8^x+8^{-x}$$-4$($4^x+4^{-x}$) を $t$ で表すと

$g(x)=($$t^{3}-3t$$)-4($$t^{2}-2$$)$

この $t$ の関数を $h(t)$ とおいて整理すると

　$h(t)=t^3-4t^2-3t+8$ $(t\text{≧}2)$　[$t$ の３次関数]

　$h'(t)=3t^2-8t-3$

　　　　$=(3t+1)(t-3)$

　$t\text{≧}2 より h'(t)=0 のとき t=3$

　これより，$h(t)$ の $t\text{≧}2$ における増減表は

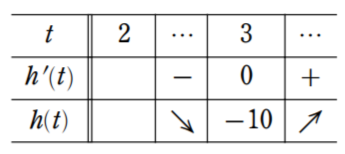
よって，$t=3$ のとき最小値 $-10$ をとる。

$t=3$ のとき，$2^x+2^{-x}=3$

これを解いて $x=-1+\log_{2}{(3\pm\sqrt{5})}$

以上より，$g(x)$ は

$x=-1+\log_{2}{(3\pm\sqrt{5})}$ (答_ウエ)

のとき最小値 $-10$ (答_オ)

解説・考え方の根拠

　標準的な典型問題である。いくつかポイントがあるので確認していく。

　まず，$2^x+2^{-x}$ の最小値を求めるとき，$(相加平均)\text{≧}(相乗平均)$ を迷わず選択できるだろうか。

$2^x+2^{-x}=$ $2^x+\frac{1}{2^{x}} (=○+\frac{定数}{○})$

であることから，$(相加平均)\text{≧}(相乗平均)$ 一択だろう。

$f(x)$ は $g(x)$ の最小値を求めるための誘導となっている。$g(x)$ は $2^x+2^{-x}=t$ とおいて，$t$ の関数として考えれば良いことには誘導がなくても気づきたい。もちろん，$t\text{≧}2$ も誘導なしで求めたい。

$g(x)=$$8^x+8^{-x}$$-4$($4^x+4^{-x}$) を $t$ で表すために，$4^x+4^{-x}$ と $8^x+8^{-x}$ を $t$ で表すことを考える。今回使った対称式の変形

$x^2+y^2=(x+y)^2-2xy$

$x^3+y^3=(x+y)^3-3xy(x+y)$

は，確実に暗記しておきたい。$t^2$ と $t^3$ を計算してもよい。

$t^2=(2^x+2^{-x})^2=4^x+4^{-x}+2$

よって　$4^x+4^{-x}=t^2-2$

$t^3=(2^x+2^{-x})^3$

　$=8^x+3・2^x+3・2^{-x}+8^{-x}$

　$=8^x+8^{-x}+3(2^x+2^{-x})$

　$=8^x+8^{-x}+3t$

よって　$8^x+8^{-x}=t^3-3t$

今回は $t$ の３次関数なので微分して，増減表から最小値を求める。

$h'(t)=(3t+1)$$(t-3)$

$3t+1>0$ であるため，$h'(t)$ の符号を決めるのは $t-3$ である。ここまで単純であればグラフを描くまでもないが，グラフから考えるのが基本であるため描いておく。

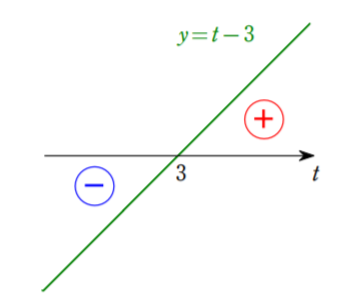
増減表から，最小値はすぐに求まる。最小値をとるときの $x$ すなわち $t=3$ のときの $x$ が必要なので求める。求めるときの式を記しておく。

$2^x+2^{-x}=3$

$2^x=u$ とおくと　$u+\frac{1}{u}=3$

$u^2-3u+1=0$

$u=\displaystyle\frac{3\pm\sqrt{5}}{2}$　[解の公式]

$2^x=\displaystyle\frac{3\pm\sqrt{5}}{2}$

$x=\log_{2}{\frac{3\pm\sqrt{5}}{2}}$　$[a^p=M\iff p=\log_{a}{M}]$

$x=\log_{2}{(3\pm\sqrt{5})}-\log_{2}{2}$

$x=\log_{2}{(3\pm\sqrt{5})}-1$

これで「解ける」へ！