等比数列の一般項，和の公式の正しい覚え方と「偶数項の等比の和」

　等比とうひ数列は等差数列と同じで「一般項」と「和」を求められるようになることが目標です。やはり，「$\sum$ (シグマ)の計算」や「漸化式ぜんかしき」でも必要になるため，正確に素早く求められるようにしましょう。
　等比数列の一般項の公式については意味を理解し，和の公式については言葉で覚えることが重要です。

　等比数列の意味や公式はもう分かってるよって人は等比数列の一般項と和に関する問題と解き方までジャンプしてしまって大丈夫です。

等比数列とは（知らない人向け）

次の $3$ つの数列は，ある規則で並んでいます。どのような規則で並んでいるか分かるでしょうか。

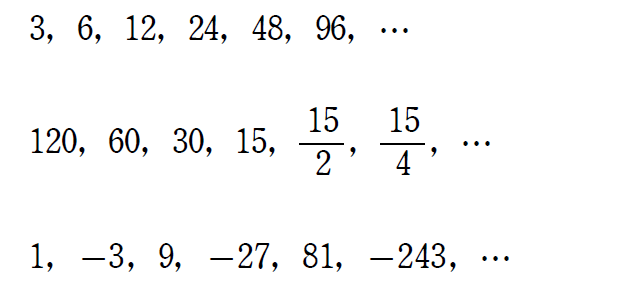
同じ数をかけ続けたものになっていることに気付きましたか。

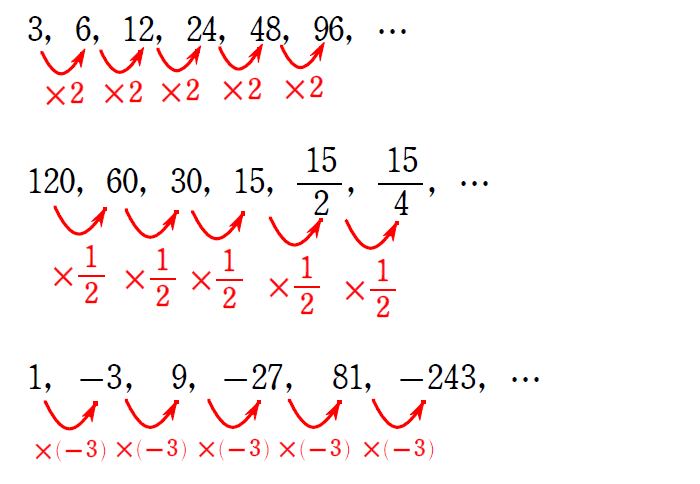
このように，同じ数をかけていく数列を等比とうひ数列といいます。
ちなみに，このかけている数を公比こうひといいます。

等比数列の定義は「隣り合う項の比が等しい数列」です。
比とは，分数にしたもので

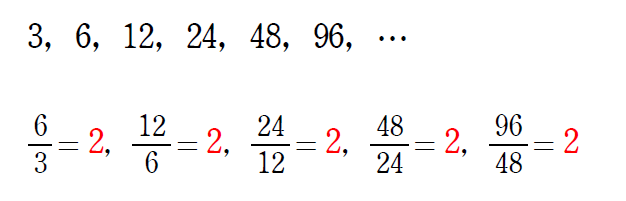
確かに等しくなっていますね。
隣り合う項の比・が等・しい数列・・で「等比数列・・・・」ということですね。
とは言え、同じ数をかけていく数列という理解で大丈夫です。

それでは，等比数列の一般項と和の求め方について考えてみましょう。

等比数列の一般項の公式

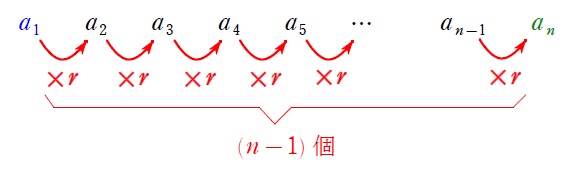
等差数列のときと同じように考えましょう。（足し算がかけ算になっただけ）

第２項 $a_2$ は 初項 $a_1$ に公比 $r$ を $1$ 回かけたもの
$a_5$ $=$ $a$ $\times$ $r$

第３項 $a_3$ は 初項 $a_1$ に公比 $r$ を $2$ 回かけたもの
$a_3$ $=$ $a$ $\times$ $r^2$

第４項 $a_4$ は 初項 $a_1$ に公比 $r$ を $3$ 回かけたもの
$a_4$ $=$ $a$ $\times$ $r^3$

第５項 $a_5$ は 初項 $a_1$ に公比 $r$ を $4$ 回かけたもの
$a_5$ $=$ $a$ $\times$ $r^4$

第 $n$ 項 $a_n$ は 初項 $a_1$ に公比 $r$ を $(n-1)$ 回かけたもの
$a_n$ $=$ $a$ $\times$ $r^{n-1}$　[等比数列の一般項の公式]

公式の丸暗記でなく，$1$ 個少ない個数だけ公比をかけているという理解が重要です。

等比数列の和の公式

初項 $a$，公比 $r$，項数 $n$ の等比数列の和 $S$
$$S=\begin{cases}na\enspace(r=1)\\ \\ \displaystyle\frac{a(1-r^n)}{1-r}=\displaystyle\frac{a(r^n-1)}{r-1}\enspace(r\not=1)\end{cases}$$  $$\left[\text{(初項)}\times\displaystyle\frac{1-\text{(公比)}^{\text{(項数)}}}{1-\text{(公比)}}\right]$$

$r\not=1$ のとき，$2$ つの式があるけど引き算を逆にしているだけで，意味は同じです。どちらを使っても良いですが，

$r<1$ であれば $S=\displaystyle\frac{a(1-r^n)}{1-r}$

$r>1$ であれば $S=\displaystyle\frac{a(r^n-1)}{r-1}$

と使い分けられるのが理想です。（分母が負にならなくて少し計算しやすい）

　等比数列の和の公式も『文字でなく言葉で覚える』ことが重要です。

　等比数列の和は「初項」「公比」「項数」から求める。特に，$n$ の部分が「項数」であることを強く意識しておきたい。（項数で間違える人がかなり多い！）

　公式の導出（証明）について確認しておきますが，ひとまずは公式を（言葉で）暗記しておけば大丈夫なので、興味がある人だけ確認してみてください。応用問題で，等比数列の和の公式の導出と同じことをする問題があるので，経験しておいて損はありません。今は導出はいいかなって人はここを押してジャンプしちゃいましょう。

＜等比数列の和の公式の導出＞
公比が 「$1$」 か 「$1$ でない」かで求め方が変わるので注意が必要。

(ア) $r=1$ のとき

$S=a+a+a+\cdots+a$

　$=a×n$　[$(\text{初項})\times(\text{項数})$]

(イ) $r\not=1$ のとき

$S=a+ar+ar^2+\cdots+ar^{n-1}$

$rS=　　ar+ar^2+\cdots+ar^{n-1}+ar^{n}$

$\text{(上)}-\text{(下)}$ とすると，間が打ち消し合って，

$S-rS=a-ar^n$

$(1-r)S=a(1-r^n)$

$(1-r)(\not=0)$ で割って

$S=\displaystyle\frac{a(1-r^n)}{1-r}$　[等比数列の和の公式]

右辺の差を入れ替えると

$S=\displaystyle\frac{a(r^n-1)}{r-1}$

等比数列の一般項と和に関する問題と解き方

　実際に，等比数列に関する問題を見てみましょう。「なぜそう考えるのか」まで含めて細かく説明します。この部分は入試問題や応用問題に対応するためには大事な部分なので，じっくり読んで自分の力にして下さい。授業を受けているような気持ちで進めてみてください。

問題

解説（授業）

(1) は等比数列の一般項を求める問題です。
等比数列の一般項を求めるために必要なものは２つですが何でしょうか。
言えますか？
はい、「初項」と「公比」ですね。

結局、「初項と公比を求める」問題なので、初項を $a$，公比を $r$ とおいて，$a$ と $r$ の関係式を２個用意しましょう。この辺りは等差数列のときと同じ発想ですね。
$a_1+a_2=24$，$a_3+a_4=6$ に着目して式を作るという方針も立てられるでしょう。
一応確認しておきますが，
$a_1=a$ (初項)，$a_2=ar$，$a_3=ar^2$，$a_4=ar^3$
ですね。$1$ 個少ない個数だけ公比 $r$ をかけている意識を大事にしましょう。
よって，
$\begin{cases}a+ar=24\\ar^2+ar^3=6 \end{cases}$
という連立方程式が得られます。
これを解くだけなのですが，慣れていないと少し難しいかも。
まず，それぞれ因数分解します。共通因数に着目して
$\begin{cases}a(1+r)=24\enspace\cdots\text{①}\\ar^2(1+r)=6\enspace\cdots\text{②}\end{cases}$
②を $r^2×$ $a(1+r)$ $=6$ と見て
① $a(1+r)=24$ を代入すると
$r^2\times$ $24$ $=6$
$r^2=\displaystyle\frac{1}{4}$
$r=\pm\displaystyle\frac{1}{2}$ となりますが，問題文に「公比が負である」と書いてありますね。見落とさないように。
$r<0$ より $r=-\displaystyle\frac{1}{2}$
$2$ 乗をとるときは，符号に注意しましょう。
① に $r=-\displaystyle\frac{1}{2}$ を代入して $a\times\displaystyle\frac{1}{2}=24$
よって　$a=48$
初項と公比が分かったので，一般項が求められますね。
初項 $48$，公比 $-\displaystyle\frac{1}{2}$ の等比数列より
$a_n=$ $48$ $\times$ $\left(-\displaystyle\frac{1}{2}\right)^{n-1}$　(答)

(2) は等比数列の和を求める問題です。
等比数列の和を求めるために必要なものは何でしょうか。
言えますか？
はい、「初項」「公比」「項数」の $3$ つですね。

$(\text{等比の和})$

$=(\text{初項})\times\displaystyle\frac{1-(\text{公比})^{(\text{項数})}}{1-(\text{公比})}$

この先，何度も出てくるので絶対に覚えてくださいね！
初項 $12$，公比 $-\displaystyle\frac{1}{2}$，項数 $8$ なので

計算がちょっとややこしそうですね。細かく途中式を入れるので一緒に頑張って計算しましょう！

$12\times\displaystyle\frac{1-\left(-\frac{1}{2}\right)^8}{1-(-\frac{1}{2})}$

$=12\times\displaystyle\frac{1–\frac{1}{256}}{\frac{3}{2}}$
　$\left[\left(-\frac{1}{2}\right)^8=\frac{1}{256}，1-\left(-\frac{1}{2}\right)=\frac{3}{2}\right]$

　$=12\times\displaystyle\frac{2}{3}\times\left(1-\displaystyle\frac{1}{256}\right)$
　[分母の $\frac{3}{2}$ は逆数にして外に出した。ここが少し難しいかも？あとで説明入れます。]

　$=8\times\displaystyle\frac{255}{256}$

　$\left[12\times\frac{2}{3}=8，1-\frac{1}{256}=\frac{255}{256}\right]$

　$=\displaystyle\frac{255}{32}$　(答)
$\left[\text{はい、できました！}\right]$

分母に分数があるときの処理の方法はいくつかありますが，以下の方法で処理できるようにしておきましょう。

$\displaystyle\frac{\text{○}}{\frac{3}{2}}=\text{○}\div \displaystyle\frac{3}{2}$　$\left[\displaystyle\frac{\text{○}}{□}=\text{○}\div \text{□}\right]$

　　$=\text{○}\times \displaystyle\frac{2}{3}$　$\left[\div\displaystyle\frac{b}{a}\text{ → }\times\displaystyle\frac{a}{b}\right]$

はじめのうちは慣れないかもしれませんが，等比数列の和ではよく出てくる計算なので，素早く正確に処理できるようにしておきましょう。

(3) 偶数項の和 $a_2+a_4+a_6+\cdots+a_{2n}$
数列の和の問題ですが，ちょっとよく分からないですね。
よく分からないときは具体的に書き出しましょう（これ大事！）。
偶数項 ($n=2,4,6,\cdots$) を求めてみると

$a_2$$=48×\left(-\displaystyle\frac{1}{2}\right)=$$-24$

$a_4$$=48×\left(-\displaystyle\frac{1}{2}\right)^3=$$-6$

$a_6$$=48×\left(-\displaystyle\frac{1}{2}\right)^5=$$-\displaystyle\frac{3}{2}$

$a_8$$=48×\left(-\displaystyle\frac{1}{2}\right)^7=$$-\displaystyle\frac{3}{8}$

$a_{10}$$=48×\left(-\displaystyle\frac{1}{2}\right)^9=$$-\displaystyle\frac{3}{32}$

よく見てみると公比が $\displaystyle\frac{1}{4}$ の等比数列になっていることに気付くでしょうか。今回は，具体的に書き出してみましたが，以下の図をイメージしてみても良いですね。

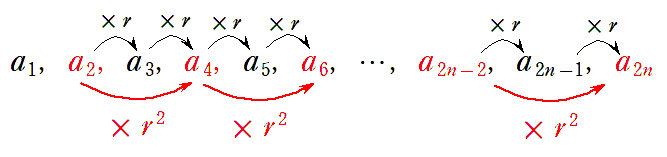
偶数項 $a_2，a_4，a_6，\cdots，a_{2n}$ に着目すると，$r$ を $2$ 回かけることで次の項になっているのが分かりますか。
つまり，偶数項は，公比が $r^2=\left(-\displaystyle\frac{1}{2}\right)^2=\displaystyle\frac{1}{4}$ の等比数列ということになりますね。

改めて，求めるものを確認しましょう。
$a_2$ $+a_4+a_6+\cdots+a_{2n}$
これは，
・初項 $a_2=-24$ (さっき求めた)
・公比 $\displaystyle\frac{1}{4}$
・項数 $n$ ($2n$ の半分)
の等比数列の和ですね。あとは公式から求めるだけです。公式は覚えてますか？

$(\text{等比の和})$

$=(\text{初項})\times\displaystyle\frac{1-(\text{公比})^{(\text{項数})}}{1-(\text{公比})}$

$-24\times\displaystyle\frac{1-(\frac{1}{4})^n}{1-(\frac{1}{4})}$

　$=-24\times\displaystyle\frac{4}{3}×\left\{1-\left(\displaystyle\frac{1}{4}\right)^{n}\right\}$
　[分母の $\frac{3}{4}$ は逆数にして外に出した]

　$=-32\left\{1-\left(\displaystyle\frac{1}{4}\right)^n\right\}$　(答)

等比数列の和は，公式が複雑で難しく感じますが，公式さえ(言葉で)覚えてしまえばただの計算問題となるので，頑張って覚えましょう！

覚えていない人は，上の言葉を声に出しながら毎日書いて覚えましょう！あ、もちろん書くのは下の公式です(笑)

$(\text{等比の和})$
$=(\text{初項})\times\displaystyle\frac{1-(\text{公比})^{(\text{項数})}}{1-(\text{公比})}$

答案

(1) 初項 $a$，公比 $r$ とする。

　$a_1+a_2=24$，$a_3+a_4=6$

　より，$\begin{cases}a+ar=24\\ar^2+ar^3=6 \end{cases}$

　$\begin{cases}a(1+r)=24\enspace\cdots\text{①}\\ar^2(1+r)=6\enspace\cdots\text{②}\end{cases}$

　②を $r^2×$ $a(1+r)$ $=6$ として

　① $a(1+r)=24$ を代入すると

　$r^2\times$ $24$ $=6$

　$r^2=\displaystyle\frac{1}{4}$

　$r<0$ より $r=-\displaystyle\frac{1}{2}$

　① より $\displaystyle\frac{1}{2}a=24$

　よって　$a=48$

　$\left[\text{初項 }48\text{，公比 }-\displaystyle\frac{1}{2}\text{ より}\right]$

　∴ $a_n=48\times\left(-\displaystyle\frac{1}{2}\right)^{n-1}$　(答)

(2) 数列 $a_{3}$，$a_{4}$，$a_{5}$，…，$a_{10}$

の和であるから，

初項 $a_3$$=48×\left(-\displaystyle\frac{1}{2}\right)^{2}=$$12$

公比 $(r=)$$-\displaystyle\frac{1}{2}$，項数 $(10-3+1=)$ $8$

の等比数列の和より，

$12\times\displaystyle\frac{1-\left(-\frac{1}{2}\right)^8}{1-(-\frac{1}{2})}$

　$=12\times\displaystyle\frac{2}{3}\times\left(1-\displaystyle\frac{1}{256}\right)$
　[分母の $\frac{3}{2}$ は逆数にして外に出した]

　$=8\times\displaystyle\frac{255}{256}$

　$=\displaystyle\frac{255}{32}$　(答)

(3) 数列 $a_{2}$，$a_{4}$，$a_{6}$，…，$a_{2n}$ は，

　初項 $a_2$$=48\times\left(-\displaystyle\frac{1}{2}\right)=$$-24$

　公比 $(r^2=)$$\displaystyle\frac{1}{4}$

　項数 $n$ であるから，和は，

　$-24\times\displaystyle\frac{1-(\frac{1}{4})^n}{1-(\frac{1}{4})}$　[等比の和]

　$=-32\left\{1-\left(\displaystyle\frac{1}{4}\right)^n\right\}$　(答)

等比数列が「解ける！」