【発展】係数が対称でない連立漸化式（一般型）の解き方

（注意）【～型】はパターンを意識するためであり，当サイト独自の表現です。答案などに書かないようにしてください。

ここでは，連立漸化式について扱いますが，係数が対称となっている連立漸化式については連立漸化式の解き方（係数が対称となっている場合）を確認してください。このページの内容は発展的な内容です。漸化式について，一通り学習した上で取り組むことをおススメします。

連立漸化式（一般型）

【一般型】$\begin{cases}a_{n+1}=pa_n+qb_n \\b_{n+1}=ra_n+sb_n \end{cases}$

連立漸化式（一般型）の解法２パターン

(例) $\begin{cases}a_{n+1}=2a_n+3b_n\\b_{n+1}=a_n-4b_n \end{cases}$

係数が対称でない場合は，普通，誘導があるため誘導に沿って解けば良い。誘導のされ方はいくつかあるが，本質的には次の２パターンです。解法[1]に誘導される場合が多い。誘導があるとは言え，初見で解ける人は多くないでしょう。一度でも経験しているかどうかで大きく差がつく問題です。

連立漸化式（一般型）の問題と解説

それでは，実際に問題を見ながら，それぞれの解法について説明していきます。

問題

(1) の解説授業（解法[1]への誘導）

$a_1=1$,  $b_1=-1$,
$\begin{cases}a_{n+1}=4a_n-2b_n\\b_{n+1}=a_n+b_n \end{cases}$

まず，問題文を見て「等比型を作って解け」と言われていることに気付かなくてはなりません。

$a_{n+1}+\alpha b_{n+1}=\beta(a_n+\alpha b_n)$

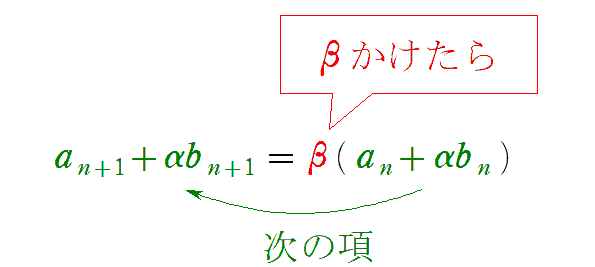
　これを満たす $\alpha ，\beta$ を求めることができれば，【等比型】と見なして，$\left\{a_n+ \alpha b_n\right\}$ の一般項を，初項 $a_1+ \alpha b_1$，公比 $\beta$ の等比数列として求めることができますね。$\alpha ，\beta$ を $2$ 組求め，それぞれ【等比型】とみなして解けば，$a_n$ と $b_n$ に関する式が $2$ つ得られるので，連立方程式のようにして $a_n$ と $b_n$ が求まります。結局のところ，この $\alpha ，\beta$ をどのようにして求めるのかを覚えてしまえば，大した問題ではありません。

　では，どのようにして $\alpha ，\beta$ を求めるかですが，
$a_{n+1}+\alpha b_{n+1}=\beta(a_n+\alpha b_n)$ $\cdots\text{①}$
において，以下の手順を行えば求まります。(この部分を暗記してしまおう！)

手順通りにしてみます。

(右辺)は展開
$\beta(a_n+\alpha b_n)=$ $\beta$$ a_n+$ $\alpha \beta$$ b_n$ $\cdots\text{②}$

(左辺)は連立漸化式を代入
$a_{n+1}=4a_n-2b_n$
$b_{n+1}=a_n+b_n$
を代入して，
$a_{n+1}+\alpha b_{n+1}$
　$=(4a_n-2b_n)+\alpha (a_n+b_n)$
　$=(4+\alpha )a_n+(\alpha -2)b_n$ $\cdots\text{③}$

そして係数比較
$\beta$$ a_n+$ $\alpha \beta$$ b_n$ $\cdots\text{②}$
$(4+\alpha )$$a_n+$ $(\alpha -2)$$b_n$ $\cdots\text{③}$
の係数を比較して，
$\beta =4+\alpha$ $\cdots\text{(＊)}$
$\alpha \beta =\alpha -2$ $\cdots\text{(＊＊)}$

あとは，この連立方程式を解くだけです。
$\text{(＊)}$ を $\text{(＊＊)}$ に代入して
$\alpha (4+\alpha )=\alpha -2$
$\alpha ^{2}+3\alpha +2=0$
$(\alpha +1)(\alpha +2)$
$\alpha =-1，-2$
$\alpha$ の値を $\text{(＊)}$ に代入して $\beta$ を求めれば，
$(\alpha ，\beta )=$ $(-1，3)$$，$$(-2，2)$
無事求まりましたね。これで，この問題は解けたも同然です。

$(\alpha ，\beta )$ の値を
$a_{n+1}+\alpha b_{n+1}=\beta(a_n+\alpha b_n)$ $\cdots\text{①}$
にそれぞれ代入することで，
$a_{n+1}-b_{n+1}=3(a_n-b_n)$ $\cdots\text{④}$【等比型】
$a_{n+1}-2b_{n+1}=2(a_n-2b_n)$ $\cdots\text{⑤}$【等比型】
の $2$ 式が得られます。

$\text{④}，\text{⑤}$ を【等比型】として，それぞれ解けますね。
④から，$\left\{a_n-b_n\right\}$ は，
初項 $a_1-b_1=2$，公比 $3$ の等比数列より
$a_n-b_n$ $=$ $2$ $\cdot$ $3^{n-1}$ $\cdots\text{④}’$

⑤から，$\left\{a_n-2b_n\right\}$ は，
初項 $a_1-2b_1=3$，公比 $2$ の等比数列より
$a_n-2b_n$ $=$ $3$ $\cdot$ $2^{n-1}$ $\cdots\text{⑤}’$

解いたものを並べて書くと，
$a_n-b_n$ $=$ $2$ $\cdot$ $3^{n-1}$ $\cdots\text{④}’$
$a_n-2b_n$ $=$ $3$ $\cdot$ $2^{n-1}$ $\cdots\text{⑤}’$

あとは，連立方程式を解くように $a_n$ と $b_n$ を求めるだけです。
差をとれば $a_n$ が消えるので，$\text{④}’-\text{⑤}’$ として $b_n$ を求めましょう。
$\text{④}’-\text{⑤}’$ より
$b_n=2\cdot 3^{n-1}-3\cdot 2^{n-1}$ (答 $b_n$)

次に，$b_n$ を $\text{④}’，\text{⑤}’$ のいずれかに代入して，$a_n$ を求めましょう。当然ですが，どちらに代入した方が簡単か意識すること。(今回は $\text{④}’$ に代入するのが良さそう）
$\text{④}’$ に $b_n$ を代入して
$a_n=2\cdot 3^{n-1}+b_n$
　 $=2\cdot 3^{n-1}+(2\cdot 3^{n-1}-3\cdot 2^{n-1})$
　 $=4\cdot 3^{n-1}-3\cdot 2^{n-1}$ (答 $a_n$)

はい，できました。
$(\alpha ，\beta )$ を求めるところまでは，知らないと難しいですが，【等比型】として解いたり，連立方程式のようにして求めたりするのは，これまでの問題でも出てきた計算ですね。特に【等比型】と見なして解く問題は，この問題に取り組んでいる人はかなり多く経験しているはずです。
結局，新しい話は $(\alpha ，\beta )$ を求めるところのみなので、この部分を意識して覚えてしまうのがポイントです。

$a_n$ は次のようにして求めても良い。

$a_n-b_n$ $=$ $2$ $\cdot$ $3^{n-1}$ $\cdots\text{④}’$
$a_n-2b_n$ $=$ $3$ $\cdot$ $2^{n-1}$ $\cdots\text{⑤}’$

($b_n$ の係数をそろえるため) $\text{④}’\times 2$より
$2a_n-2b_n$ $=$ $4$ $\cdot$ $3^{n-1}$ $\cdots\text{④}^{”}$
$\text{④}^{”}-\text{⑤}’$ より，
$a_n=4\cdot 3^{n-1}-3\cdot 2^{n-1}$

どちらが簡単かは状況によるので，どちらもできるようにして使い分けられるのが理想。

(1) の答案(解法[1]への誘導)

 $a_{n+1}+\alpha b_{n+1}=\beta(a_n+\alpha b_n)$ $\cdots\text{①}$

①の右辺を展開すると，
$\beta(a_n+\alpha b_n)=$ $\beta$$ a_n+$ $\alpha \beta$$ b_n$ $\cdots\text{②}$

一方，①の左辺に漸化式を代入すると，
$a_{n+1}+\alpha b_{n+1}$
　$=(4a_n-2b_n)+\alpha (a_n+b_n)$
　$=(4+\alpha )a_n+(\alpha -2)b_n$ $\cdots\text{③}$

②，③の係数を比較して
$\begin{cases}\beta =4+\alpha \\ \alpha \beta =\alpha -2 \end{cases}$
これを解いて，
$(\alpha ，\beta )=(-1，3)，(-2，2)$

$(\alpha ，\beta )$ を①にそれぞれ代入して
$a_{n+1}-b_{n+1}=3(a_n-b_n)$ $\cdots\text{④}$【等比型】
$a_{n+1}-2b_{n+1}=2(a_n-2b_n)$ $\cdots\text{⑤}$【等比型】

④から，$\left\{a_n-b_n\right\}$ は，
初項 $a_1-b_1=2$，公比 $3$ の等比数列より
$a_n-b_n$ $=$ $2$ $\cdot$ $3^{n-1}$ $\cdots\text{④}’$

⑤から，$\left\{a_n-2b_n\right\}$ は，
初項 $a_1-2b_1=3$，公比 $2$ の等比数列より
$a_n-2b_n$ $=$ $3$ $\cdot$ $2^{n-1}$ $\cdots\text{⑤}’$

$\text{④}’-\text{⑤}’$ より
$b_n=2\cdot 3^{n-1}-3\cdot 2^{n-1}$ (答 $b_n$)

$\text{④}’$ より
$a_n=2\cdot 3^{n-1}+b_n$
　 $=2\cdot 3^{n-1}+(2\cdot 3^{n-1}-3\cdot 2^{n-1})$
　 $=4\cdot 3^{n-1}-3\cdot 2^{n-1}$ (答 $a_n$)

(2) の解説授業（解法[2]への誘導）

$a_1=1$,  $b_1=-1$,
$\begin{cases}a_{n+1}=4a_n-2b_n\\b_{n+1}=a_n+b_n \end{cases}$

まず，$a_{n+2}$ が必要なので，
$a_{n+1}=4a_n-2b_n$ の $n$ を 1 つずつ進め，
$a_{n+2}=4a_{n+1}-2b_{n+1}$
とします。

ここで，$b_{n+1}$ と $b_{n}$ を消去したいので， 連立漸化式から以下のように変形します。
$b_{n+1}=a_n+b_n$
これで $b_{n+1}$ が消去できますが，$b_n$ が残ってしまいますね。
よって，
$a_{n+1}=4a_n-2b_n$ から
$b_n=\displaystyle\frac{1}{2}(-a_{n+1}+4a_n)$
とします。
これで，$a_{n+2}$,  $a_{n+1}$, $a_{n}$ のみの式になりますね。

$a_{n+2}=4a_{n+1}-2$$b_{n+1}$
　$=4a_{n+1}-2$$(a_n+b_n)$
　$=4a_{n+1}-2a_n-2$$b_n$
　$=4a_{n+1}-2a_n-2$ $\cdot$ $\displaystyle\frac{1}{2}(-a_{n+1}+4a_n)$
　$=5a_{n+1}-6a_n$
(この部分が慣れていないと意外と難しいので，繰り返し計算して習得しましょう)

整理して，
$a_{n+2}-5a_{n+1}+6a_n=0$【隣接３項間型】
となるので，隣接３項間型の漸化式が解けるかどうかの問題となりますね。
$a_n$ を求める手順は答案の通りなので省略します。隣接３項間型の漸化式の解法が怪しい場合は，まず以下の記事の内容から取り組むべきです。

$a_n$ を求めると，
$a_n=4\cdot 3^{n-1}-3\cdot 2^{n-1}$

次に $b_n$ を求めます。
$a_n$ が分かっているので，
$b_n=\displaystyle\frac{1}{2}(-a_{n+1}+4a_n)$
に代入すれば $b_n$ は求まりますが，計算がやや面倒であるためミスしないように慎重に計算しましょう。ここまでできてミスしたらもったいないですからね！

$b_n=\displaystyle\frac{1}{2}(-$$a_{n+1}$$+4$$a_n$$)$
　　$=-\displaystyle\frac{1}{2}$$a_{n+1}$ $+$ $2$$a_n$
であるから，$a_{n}$ と $a_{n+1}$ を代入します。

$a_n=4\cdot 3^{n-1}-3\cdot 2^{n-1}$
$a_{n+1}$ $=4\cdot 3^{n}-3\cdot 2^{n}$
　 　$=12\cdot 3^{n-1}-6\cdot 2^{n-1}$
[指数を $n-1$ にそろえておくと計算しやすい]

よって，
$b_n=-\displaystyle\frac{1}{2}$$(12\cdot 3^{n-1}-6\cdot 2^{n-1})$

　　　　 $+$ $2$$(4\cdot 3^{n-1}-3\cdot 2^{n-1})$

　　$=-6\cdot 3^{n-1}+3\cdot 2^{n-1}$
　　　　$+8\cdot 3^{n-1}-6\cdot 2^{n-1}$
よって，
$b_n=2\cdot 3^{n-1}-3\cdot 2^{n-1}$　(答 $b_n$)

なんとかできました。
隣接３項間型の漸化式の解き方さえ身に付いていれば発想はしやすいですが，計算がやや面倒です。もし誘導がないのであれば解法[1]で解けるようにしておきたいです。誘導も解法[1]への誘導が多いため，重要度は解法[1]の方が上です。

(2) の答案（解法[2]への誘導）

$a_{n+1}=4a_n-2b_n$ $\cdots\text{①}$
$b_{n+1}=a_n+b_n$

①より $b_n=\displaystyle\frac{1}{2}(-a_{n+1}+4a_n)$

よって，①から
$a_{n+2}=4a_{n+1}-2$$b_{n+1}$
　$=4a_{n+1}-2$$(a_n+b_n)$
　$=4a_{n+1}-2a_n-2$$b_n$
　$=4a_{n+1}-2a_n-2$ $\cdot$ $\displaystyle\frac{1}{2}(-a_{n+1}+4a_n)$
　$=5a_{n+1}-6a_n$
したがって，
$a_{n+2}-5a_{n+1}+6a_n=0$【隣接３項間型】

$\begin{cases}a_{n+2}-2a_{n+1}\\　=3(a_{n+1}-2a_n)\cdots\text{②}\\ \\a_{n+2}-3a_{n+1}\\　=2(a_{n+1}-3a_n)\cdots\text{③}\end{cases}$ 【等比型】

①より $a_2=4a_1-2b_1=6$ であるから，

$\begin{cases}a_2-2a_1=4\\a_2-3a_1=3\end{cases}$　[初項の確認]

よって，②，③より

$\begin{cases}a_{n+1}-2a_n=4\cdot 3^{n-1}\cdots\text{④}\\a_{n+1}-3a_n=3\cdot 2^{n-1}\cdots\text{⑤}\end{cases}$

$\text{④}-\text{⑤}$ より
$a_n=4\cdot 3^{n-1}-3\cdot 2^{n-1}$ (答 $a_n$)

$a_{n+1}=4\cdot 3^{n}-3\cdot 2^{n}$
　 　$=12\cdot 3^{n-1}-6\cdot 2^{n-1}$
であるから，
$b_n=\displaystyle\frac{1}{2}(-a_{n+1}+4a_n)$ より

$b_n=2\cdot 3^{n-1}-3\cdot 2^{n-1}$ (答 $b_n$)

連立漸化式（一般型）がこれで「解ける！」

【一般型】$\begin{cases}a_{n+1}=pa_n+qb_n \\b_{n+1}=ra_n+sb_n \end{cases}$