(注意)【~型】はパターンを意識するためであり,当サイト独自の表現です。答案などに書かないようにしてください。
ここでは連立漸化式のうち,係数が対称となっているものを扱います。係数が対称というと特別な場合のように感じるかもしれませんが,入試ではむしろ頻出なので,優先度は高いです。解法さえ知っていれば難しくないので,しっかり確認しましょう。係数が対称でない連立漸化式の解き方を確認したい人は【発展】係数が対称でない連立漸化式(一般型)の解き方をご覧ください。
連立漸化式(対称係数型)
【対称係数型】$\begin{cases}a_{n+1}=pa_n+qb_n \\b_{n+1}=qa_n+pb_n \end{cases}$
(例) 係数が対称
$\begin{cases}a_{n+1}=2a_n+5b_n\\b_{n+1}=5a_n+2b_n \end{cases}$
連立漸化式(対称係数型)の解法
係数が対称の場合の連立漸化式は,以下のことをパターンとして暗記しておく。
連立漸化式(対称係数)の問題と解説
それでは,実際の問題の解説の中で詳しく説明していきますね。
問題
解説(授業)
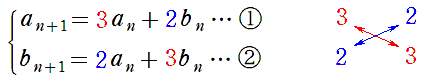
係数が対称なので,
和$(①+②)$ と 差$(①-②)$ をとって,
$\left\{a_n+b_n\right\}$ と $\left\{a_n-b_n\right\}$ をそれぞれ【等比型】とみる!
という方針で解きます。
$①+②$ を考えてみると,
$a_{n+1}+b_{n+1}=5(a_n+b_n)$【等比型】
となりますが,$a_n+b_n$ をひとかたまりと見れば
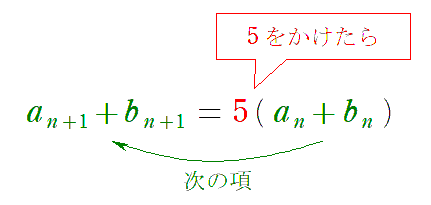
よって,$\left\{a_n+b_n\right\}$ は,
初項 $a_1+b_1=3$,公比 $5$ の等比数列より,
$a_n+b_n$ $=$ $3$ $\cdot$ $5^{n-1}$ ・・・③
同様にして,$①-②$ を考えてみると,
$a_{n+1}-b_{n+1}=a_n-b_n$【等比型】
よって,$\left\{a_n-b_n\right\}$ は,
初項 $a_1-b_1=-1$,公比 $1$ の等比数列より,
$a_n-b_n$ $=$ $-1$ $\cdot$ $1^{n-1}$
したがって,
$a_n-b_n=-1$ ・・・④
となりますね。
$a_{n+1}-b_{n+1}=a_n-b_n$ を【等比型】として解きましたが,今回の場合は以下のように考えると,より簡単に求まります。
$a_n-b_n=a_{n-1}-b_{n-1}$
$=・・・=a_1-b_1=-1$
一瞬ですね。何をしているか分かりますか?
一般に $a_{n+1}=a_n$ のとき $\left\{a_n\right\}$ は定数列(ずっと同じ数が続く数列)となり,$a_n=a_1$ となります。

今回の場合,$a_{n+1}-b_{n+1}=a_n-b_n$ という式を見て $\left\{a_n-b_n\right\}$ が定数列となっていることに気付けば,初項だけ考えれば一般項 $a_n-b_n$ が求まるということですね。
さて,
和と差をとることで,
$a_n+b_n=3\cdot5^{n-1}$ …③
$a_n-b_n=-1$ …④
という $2$ 式が得られますが,このあとどうすれば $a_n$ と $b_n$ が求まるか分かりますか?
分からないものが $a_n$ と $b_n$ の $2$ つ,
式が $2$ つ
の状態なので,連立方程式を解くように求めれば良さそうですね。
(分からないものの個数だけ式を用意すれば求まるというのが,数学における最重要事項の $1$ つでしたね)
$③+④$ より $b_n$ を消去して
$2a_n=3\cdot5^{n-1}-1$
$2$ で割って
$a_n=\displaystyle\frac{1}{2}(3\cdot5^{n-1}-1)$ (答 $a_n$)
$③-④$ より $a_n$ を消去して
$2b_n=3\cdot5^{n-1}+1$
$2$ で割って
$b_n=\displaystyle\frac{1}{2}(3\cdot5^{n-1}+1)$ (答 $b_n$)
解けましたね。和と差をとることさえ知識として入れておけば,特に難しくない問題ですね。
絶対に落とせないレベルの問題であるため,確実に解けるようにしておきましょう。
(参考) $b_n$ は次のように求めてもよい
$a_n=\displaystyle\frac{1}{2}(3\cdot5^{n-1}-1)$
を求めたあと,
$a_n-b_n=-1$ …④
より,
$b_n$ $=$ $a_n$ $+$ $1$
よって,
$b_n$ $=$ $\displaystyle\frac{1}{2}(3\cdot5^{n-1}-1)$ $+$ $1$
$=\displaystyle\frac{1}{2}(3\cdot5^{n-1}-1+2)$
$=\displaystyle\frac{1}{2}(3\cdot5^{n-1}+1)$
答案
$a_{n+1}=3a_n+2b_n$ ・・・①
$b_{n+1}=2a_n+3b_n$ ・・・②
$①+②$ より,
$a_{n+1}+b_{n+1}=5(a_n+b_n)$ 【等比型】
$\left\{a_n+b_n\right\}$ は,
初項 $a_1+b_1=3$,公比 $5$ の等比数列より,
$a_n+b_n=3\cdot5^{n-1}$ …③
$①-②$ より,
$a_{n+1}-b_{n+1}=1(a_n-b_n)$ 【等比型】
$\left\{a_n-b_n\right\}$ は,
初項 $a_1-b_1=-1$,公比 $1$ の等比数列より,
$a_n-b_n=-1\cdot1^{n-1}$
∴ $a_n-b_n=-1$ …④
③,④ より
$a_n=\displaystyle\frac{1}{2}(3\cdot5^{n-1}-1)$
$b_n=\displaystyle\frac{1}{2}(3\cdot5^{n-1}+1)$ (答)
連立漸化式(対称係数型)がこれで「解ける!」
【対称係数型】$\begin{cases}a_{n+1}=pa_n+qb_n \\b_{n+1}=qa_n+pb_n \end{cases}$

