(注意)【~型】はパターンを意識するためのもので当サイト独自の表現です。答案などには書かないようにしてください。
ここでは,対数を利用して解く漸化式について扱います。まず,どういう形のときに対数を利用するのか知り,次に,対数をとったあとどう解くのか実際の問題の解説で確認していきます。
【対数利用型】積$a_{n+1}a_n$,累乗$\left(a_{n}\right)^{○}$,累乗根$\sqrt[○]{a_n}$ を含む漸化式
(例) $a_{n+1}=2a_n^{\enspace3}$
(例) $a_{n}a_{n+1}=2\sqrt{a_n}$
【対数利用型】漸化式の解法
例のように,積$a_{n+1}a_n$,累乗$\left(a_{n}\right)^{\text{○}}$,累乗根$\sqrt[\text{○}]{a_n}$ を含む漸化式は,次のようにして解きます。
対数(例えば底2)をとることにより,対数の性質から
$\log_{2}{a_{n+1}a_n}=\log_{2}{a_{n+1}}+\log_{2}{a_n}$
$\log_{2}{a_{n}^{\enspace p}}=p\log_{2}{a_n}$
$\log_{2}{\sqrt[q]{a_n}}=\displaystyle\frac{1}{q}\log_{2}{a_n}$
とバラバラにすることができて,うまいこと行きます。
誘導が入る場合もありますが,なくても解けるようにしておきたい問題です。
また,底をいくつで考えれば良いかは問題の解説で触れますね。
対数を利用する漸化式の問題と解説
それでは,実際に問題を見てみましょう。
問題
$a_1=2$,$a_{n+1}=8a_n^{\enspace 2}$
解説(授業)
$a_{n+1}=8$$a_n^{\enspace2}$
累乗 $a_n^{\enspace2}$ があるので対数をとるパターンですね。これは,見抜けるようにしないとダメですよ。今回は底 $2$ の対数とって $\log_{2}{a_n}=b_n$ とおく方針で解きましょう。
(なぜ底を $2$ にするかはあとで説明します)
漸化式に限らず,対数をとるときは,両辺が正であることを言う必要があります。なぜか分かりますか?
はい,真数条件(真数は正)ですね。
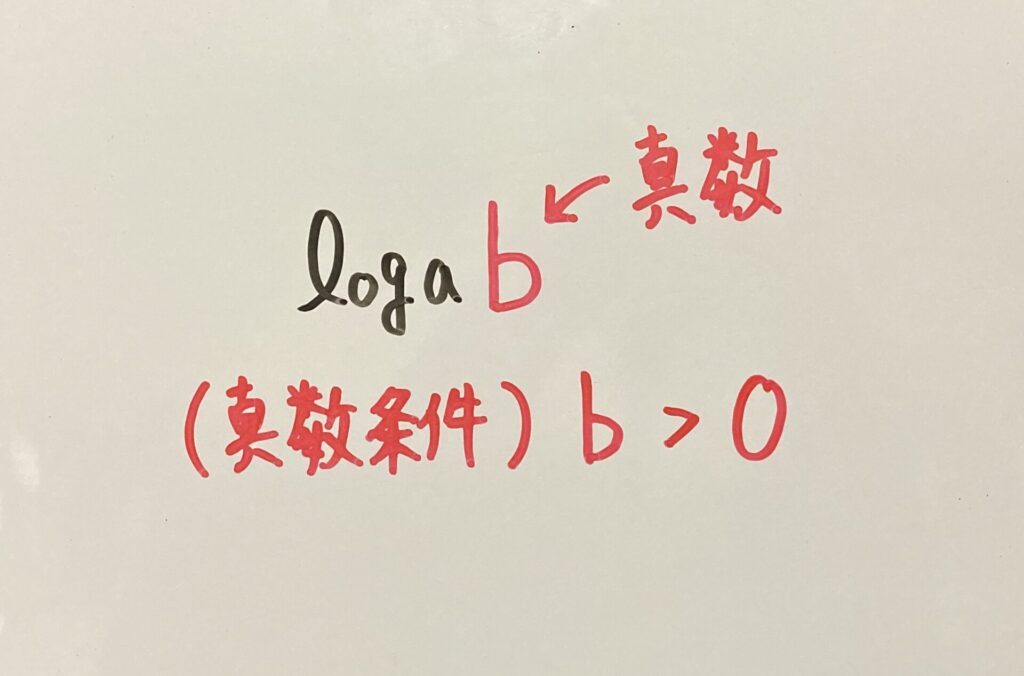
対数をとると,式の部分がそのまま真数になるため,正であることを言っておかないとマズイのです。
難しそうですが,「初項と漸化式から両辺は正」と書いておけば十分です。
もし,証明を求められた場合は,背理法や数学的帰納法を用いると良いでしょう。
それでは,実際に解いてみましょう。
$a_1=2$,$a_{n+1}=8a_n^{\enspace2}$
初項と漸化式から両辺は正であるから,底 $2$ の対数をとって,
$\log_{2}{a_{n+1}}=$ $\log_{2}{8a_n^{\enspace2}}$
(右辺について)
$\log_{2}{8a_n^{\enspace2}}$
$=\log_{2}{8}+\log_{2}{a_n^{\enspace2}}$
$=\log_{2}{2^3}+2\log_{2}{a_n}$
$=3+2\log_{2}{a_n}$
として,
$\log_{2}{a_{n+1}}=2\log_{2}{a_n}+3$
$\log_{2}{a_n}=b_n$ とおくと,
$b_{n+1}$ $=2$$b_{n}$ $+3$
これは解けますよね?どうすれば良いか,すぐに言えないとダメな型ですよ?
はい【特殊解型】ですね。漸化式の最重要パターンでした。
初項 $b_1$ が必要になるので,求めておきましょう。
$b_1=\log_{2}{a_1}=\log_{2}{2}=1$ ですね。
$\alpha=2\alpha+3$ を解くと $\alpha=-3$ より
$b_{n+1}+3=2(b_n+3)$ 【等比型】
と変形できますね。よって,
$\left\{b_n+3\right\}$ は,
初項 $b_1+3=1+3=4$,公比 $2$ の等比数列より
$b_n+3$ $=$ $4$ $\cdot$ $2^{n-1}$ $=2^{n+1}$
したがって,$3$ を移項して
$b_n=2^{n+1}-3$
あとは,
$\log_{2}{a_n}=b_n$ から $a_n=2^{b_n}$ として,$a_n$ を求めましょう。
$a_n=2^{2^{n+1}-3}$ (答)
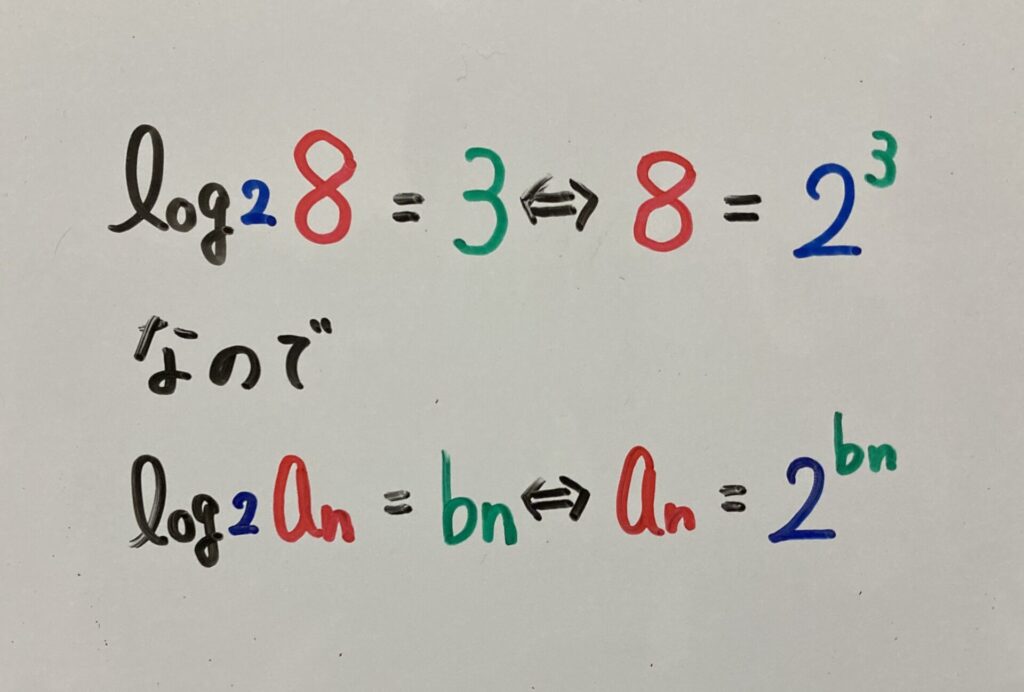
はい,解けましたね!
さて,今回は底を $2$ にして考えましたが根拠は何でしょうか。底については「初項や漸化式を見て適当に決める」ようにしてください。え?適当?と思うかもしれませんが,はい,適当です。うまいこといきそうなものを選べばいいんです。それだと困ると思うので,迷ったら「$\left\{a_n\right\}$ の初項 $a_1$ を底」にしてみてください。だいたいうまくいきます。
とりあえず適当に決めて,もし途中で都合が悪くなったら書き直せばいいんです。
例えば,今回の問題でとりあえず底を $3$ で考えると以下のようになります。
$\log_{3}{a_{n+1}}=2\log_{3}{a_n}$ $+$ $3\log_{3}{2}$
$\log_{3}{a_n}=b_n$ とおくと,
$b_1=\log_{3}{a_1}$ $=$ $\log_{3}{2}$
こうなると「底 $2$ にすれば良かった」と思いますよね。
ということで,底を $2$ に書き直せば解決です。
答案
$a_{n+1}=8a_n^{\enspace2}$ 【対数利用型】
初項と漸化式から両辺は正なので,
底 $2$ の対数とって,
$\log_{2}{a_{n+1}}=\log_{2}{8a_n^{\enspace2}}$
よって,
$\log_{2}{a_{n+1}}=2\log_{2}{a_n}+3$
$\log_{2}{a_n}=b_n$ とおくと,
$b_{n+1}$ $=2$$b_{n}$ $+3$ 【特殊解型】
変形して,
$b_{n+1}+3=2(b_n+3)$ 【等比型】
[$\alpha=2\alpha+3$ を解くと $\alpha=-3$]
$b_1=\log_{2}{a_1}=\log_{2}{2}=1$ より,
$\left\{b_n+3\right\}$ は,
初項 $b_1+3=1+3=4$,
公比 $2$ の等比数列より,
$b_n+3$ $=$ $4$ $\cdot$ $2^{n-1}$ $=2^{n+1}$
よって,$b_n=2^{n+1}-3$
$\log_{2}{a_n}=b_n$ より $a_n=2^{b_n}$ であるから,
$a_n=2^{2^{n+1}-3}$ (答)
$a_n$ の積,累乗,累乗根を含む漸化式がこれで「解ける!」
【対数利用型】積$a_{n+1}a_n$,累乗$\left(a_{n}\right)^{○}$,累乗根$\sqrt[○]{a_n}$ を含む漸化式

