$\sum$ の全パターンを確認したい人→∑(シグマ)の公式と∑の計算全パターン。すべての∑に対応するための考え方
$\sum$ に関する基本事項について確認していきましょう。
①と②はもう大丈夫だから問題を確認したいという人は$\sum$ の計算について(基本)までジャンプ!
①は大丈夫だから公式から確認したいという人は$\sum$ の公式や性質についてまでジャンプ!
最初からしっかり確認したいって人はこのまま順番に確認してみてください!
$\sum$ って何?読み方や定義について
$\sum$ の読み方は「シグマ」、アルファベット「S」のギリシャ文字です。「和」は英語で「sum」なのでその頭文字の「S」は,数学ではよく和を表すときに使いますね。実はこの「$\sum$」も和を表す記号として使われます。それでは,$\sum$ の定義について説明します。
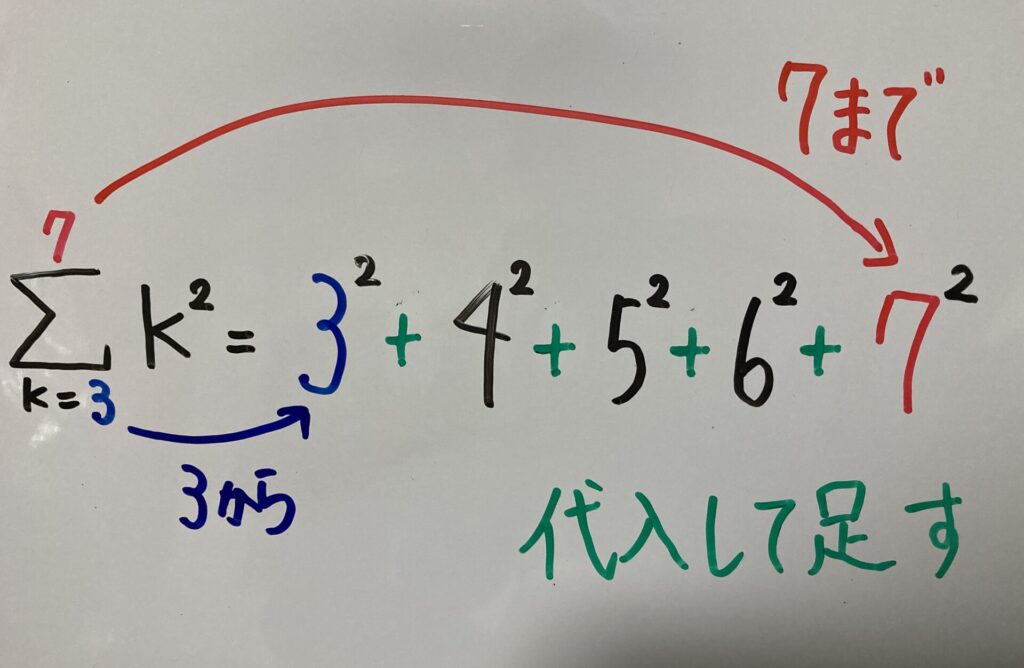
いくつか例を書くので,どういう意味なのか式を見ながら納得してください。
$\displaystyle\sum_{k=1}^{n}{a_k}=a_1+a_2+a_3+\cdots+a_n$
$\displaystyle\sum_{k=3}^{7}{a_k}=a_3+a_4+a_5+a_6+a_7$
$\displaystyle\sum_{k=0}^{9}{k^2}=0^2+1^2+2^2+\cdots+9^2$
$\displaystyle\sum_{k=1}^{n+1}{\displaystyle\frac{1}{k}}=$$\displaystyle\frac{1}{1}+\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}+\cdots+\displaystyle\frac{1}{n+1}$
$\displaystyle\sum_{k=1}^{4}{3}=3+3+3+3$
$k$ の部分にどんどん代入して足していくだけです!簡単ですね!
$k$ 以外の部分は変化しないので,$k$ がない最後の例は同じ数字を足すだけになっていますね。
$\sum$ の公式や性質について
次に $\sum$ の覚えるべき公式や性質について説明していきます。
公式は基本的には暗記しておけば良いのですが,暗記の仕方に気を付けて欲しいのと,一部,意味を理解しておくと計算がぐっとラクになる部分があるので,丸暗記しちゃってますという人はぜひ確認してください。
$\sum$ の公式と覚え方
[1] $\displaystyle\sum_{k=1}^{n}{c}=cn$
[2] $\displaystyle\sum_{k=1}^{n}{k}=\displaystyle\frac{1}{2}n\left(n+1\right)$
[3] $\displaystyle\sum_{k=1}^{n}{k^2}=\displaystyle\frac{1}{6}n\left(n+1\right)(2n+1)$
[4] $\displaystyle\sum_{k=1}^{n}{k^3}=\left\{\displaystyle\frac{1}{2}n\left(n+1\right)\right\}^2$
$=\displaystyle\frac{1}{4}n^2\left(n+1\right)^2$
[5] $\displaystyle\sum_{k=1}^{n}{r^{k-1}}=\displaystyle\frac{1-r^n}{1-r}$ [等比の和]
[4]は[2]を$2$ 乗したものと覚えておくと覚えすいですね。
$\displaystyle\sum_{k=1}^{n}{k^3}=\left(\displaystyle\sum_{k=1}^{n}{k}\right)^2$
[2]と[3]は次のように覚えておきましょう。

$\sum$ の公式で計算ができる式
[1] 定数 (例) $\displaystyle\sum_{k=1}^{n}{3}$
[2] $k$ の1次式 (例) $\displaystyle\sum_{k=1}^{n}{(2k-1)}$
[3] $k$ の2次式 (例) $\displaystyle\sum_{k=1}^{n}{(3k^2+k)}$
[4] $k$ の3次式 (例) $\displaystyle\sum_{k=1}^{n}{(4k^3-2)}$
[5] $(\text{定数})^k$ (例) $\displaystyle\sum_{k=1}^{n}{3^k}$
上記の形であれば,公式から計算できます。これら以外の形は工夫して求める必要があります。それがどうしたの?って思う人も多いと思いますが,そのまま計算できるのかできないのかの判断はかなり重要です。式を見たとき,頑張って計算すればいいのか,計算の前に何か変形しないといけないのかを判断する癖をつけておかないと,計算できるのに無駄に変形しようとしたり,そのままでは計算できないのに無理して計算しようとしたりして,タイムロスや間違いに繋がります。そのまま計算できるのは案外少なく,上記をまとめると次のようになります。
$k$ の $3$ 次以下の式と$(\text{定数})^k$ だけ!
やっていいことと、やっちゃダメなこと
<やっていいこと>
○ $\displaystyle\sum_{}^{}{(a_k\pm b_k)}=\displaystyle\sum_{}^{}{a_k}\pm\displaystyle\sum_{}^{}{b_k}$
[足し算,引き算をバラす(まとめる)]
○ $\displaystyle\sum_{}^{}{2a_k}=2\displaystyle\sum_{}^{}{a_k}$
[定数を外に出す(中に入れる)]
<(よく見る)やっちゃダメなこと>
× $\displaystyle\sum_{}^{}{a_kb_k}=\displaystyle\sum_{}^{}{a_k}\displaystyle\sum_{}^{}{b_k}$
[かけ算をバラす(まとめる)のはダメ]
× $\displaystyle\sum_{}^{}{\displaystyle\frac{a_k}{b_k}}=\displaystyle\frac{\displaystyle\sum_{}^{}{a_k}}{\displaystyle\sum_{}^{}{b_k}}$
[分数をバラす(まとめる)のはダメ]
×$\displaystyle\sum_{k=1}^{n}{\displaystyle\frac{1}{k}}=\displaystyle\frac{1}{\displaystyle\sum_{k=1}^{n}{k}}=\displaystyle\frac{1}{\displaystyle\frac{1}{2}n\left(n+1\right)}$
これはダメ!
$\sum$ の公式ではなく意味を理解して計算した方が良いもの
[1],[2],[5] は公式にあてはめるより,意味を理解して計算した方が早く,ミスも減らせます。
[1] $\displaystyle\sum_{k=1}^{n}{c}$
$=c+c+c+\cdots+c$ ($c$ が $n$ 個)
$=cn$
(例) $\displaystyle\sum_{k=2}^{n-1}{3}$
$2$ ~ $n-1$ の項数は $(n-1)-2+1=n-2$
なので,$\displaystyle\sum_{k=2}^{n-1}{3}=3\times(n-2)$
[2] $\displaystyle\sum_{k=1}^{n}{k}=1+2+3+\cdots+n$
これは,初項 $1$,末項 $n$,項数 $n$ の等差数列の和なので,
$\displaystyle\sum_{k=1}^{n}{k}=\displaystyle\frac{1}{2}\times n\times(1+n)$
(例) $\displaystyle\sum_{k=1}^{n}{(2k-1)}$
$\displaystyle\sum_{k=1}^{n}{(2k-1)}=1+3+5+\cdots+(2n-1)$
(初項 $1$,末項 $2n-1$,項数 $n$ の等差数列の和なので)
$=\displaystyle\frac{1}{2}\times n\times\left\{1+(2n-1)\right\}$
$=\displaystyle\frac{1}{2}\times n\times(2n)$
$=n^2$
[5] $\displaystyle\sum_{k=1}^{n}{r^{k-1}}=1+r+r^2+\cdots+r^{n-1}$
これは,初項 $1$,公比 $r$,項数 $n$ の等比数列の和なので,
$\displaystyle\sum_{k=1}^{n}{r^{k-1}}=1\times\displaystyle\frac{1-r^n}{1-r}$
$=\displaystyle\frac{1-r^n}{1-r}$
(例) $\displaystyle\sum_{k=1}^{n}{2^{k}}$
$\displaystyle\sum_{k=1}^{n}{2^{k}}=2+4+8+\cdots+2^{k}$
(初項 $2$,公比 $2$,項数 $n$ の等比数列の和なので)
$=2\times\displaystyle\frac{2^{n}-1}{2-1}$
$=2\times \left(2^{n}-1\right)$
$=2^{n+1}-2$
$\sum$ の計算について(基本)
実際に問題を見てみましょう。基本問題なので,公式さえ頭に入っていれば難しくはない問題ですが,ここの計算で間違った理解があると,以降の内容で苦労します。正しい計算方法について確認しましょう。
問題
(1) $\displaystyle\sum_{k=1}^{n}{k(4k^2-k+1)}$
(2) $\displaystyle\sum_{k=0}^{n}{(3k+1)}$
(3) $\displaystyle\sum_{k=2}^{n-1}{3^{k+1}}$
解説(授業)
(1) $\displaystyle\sum_{k=1}^{n}{k(4k^2-k+1)}$
かけ算の形になっているので,まずは展開しましょう。
$\displaystyle\sum_{k=1}^{n}{k(4k^2-k+1)}=\displaystyle\sum_{k=1}^{n}{(4k^3-k^2+k)}$
足し算と引き算はバラバラに,定数は外に出せるので,
$\displaystyle\sum_{k=1}^{n}{(4k^3-k^2+k)}$ $=4\displaystyle\sum_{k=1}^{n}{k^3}-\displaystyle\sum_{k=1}^{n}{k^2}+\displaystyle\sum_{k=1}^{n}{k}$
(この部分の計算は慣れてきたら省略しましょう。答案では灰色にしておきます。)
あとは,$\sum$ の公式を適用して地道に計算しましょう。
・$\displaystyle\sum_{k=1}^{n}{k^3}=\displaystyle\frac{1}{4}n^2\left(n+1\right)^2$
・$\displaystyle\sum_{k=1}^{n}{k^2}=\displaystyle\frac{1}{6}n\left(n+1\right)(2n+1)$
・$\displaystyle\sum_{k=1}^{n}{k}=\displaystyle\frac{1}{2}n\left(n+1\right)$
$4$$\displaystyle\sum_{k=1}^{n}{k^3}$ $-$ $\displaystyle\sum_{k=1}^{n}{k^2}$ $+$ $\displaystyle\sum_{k=1}^{n}{k}$
$=4$ $\cdot$ $\displaystyle\frac{1}{4}n^2(n+1)^2$
$-$ $\displaystyle\frac{1}{6}n(n+1)(2n+1)$
$+$ $\displaystyle\frac{1}{2}n(n+1)$
$=n^2(n+1)^2$
$-\displaystyle\frac{1}{6}n(n+1)(2n+1)$
$+\displaystyle\frac{1}{2}n(n+1)$
公式適用後は、因数分解していく方針で計算します。
このとき,次のことを意識して進めましょう。
・カッコ内が整数となるように分数でくくる(分母の最小公倍数に着目)
$n^2(n+1)^2$
$-\displaystyle\frac{1}{6}n(n+1)(2n+1)$
$+\displaystyle\frac{1}{2}n(n+1)$
・$n(n+1)\text{ が共通因数}$
・$2$ と $6$ の最小公倍数が $6$
だから $\displaystyle\frac{1}{6}n(n+1)$ でくくって
$=\displaystyle\frac{1}{6}n(n+1)\left\{6n(n+1)-(2n+1)+3\right\}$
$=\displaystyle\frac{1}{6}n(n+1)(6n^2+4n+2)$
$=\displaystyle\frac{1}{3}n(n+1)(3n^2+2n+1)$ (答)
キツイ計算だったので,検算もしておきましょう。
計算結果において $n=1$ を代入する。
$\displaystyle\frac{1}{3}\times1\times2\times6=4$
これが,もとの式において $n=1$ を代入した値,すなわち,$k$ の式に $k=1$ を代入した値と一致していることを確認しましょう。
$k(4k^2-k+1)$$=4\times1^2-1+1$$=4$
偶然一致する可能性もあるけど,最低限確認しておいた方が良いでしょう。
例えば,この計算結果を使って以降の問題を解くような場合であれば,最初で間違えていたら,以降全滅です。前にも話しましたが,数列分野は検算が可能な分野です。試験時間との兼ね合いもありますが,少しの時間でミスを見つけられるなら,やっておいて損はないでしょう。
(2) $\displaystyle\sum_{k=0}^{n}{(3k+1)}$
さて、まずはバラバラにしよう!…はダメですよ?
じゃあ、そこは省略してすぐに $\sum$ の公式を適用!…ダメです!
今回,着目すべき部分は $3k+1$ が $k$ の $1$ 次式であるという点です。
等差数列の和は「初項」「末項」「項数」の $3$ つに着目!
初項は $k=0$ を代入したもの
末項は $k=n$ を代入したもの
項数は $n-0+1=n+1$
ですね。

よって,求める和は,
初項 $1$,末項 $3n+1$,項数 $n+1$ の等差数列の和より,
$=\displaystyle\frac{1}{2}\times \text{(項数)}\times \text{(初項+末項)}$
$\displaystyle\sum_{k=0}^{n}{(3k+1)}$
$=\displaystyle\frac{1}{2}×(n+1)×\left\{1+(3n+1)\right\}$
$=\displaystyle\frac{1}{2}(n+1)(3n+2)$ (答)
はい、できました!
等差数列の和について抜けている人は以下の記事で確認してください。
ちなみに,これを $\sum$ の公式で求める場合は以下のようになります。
$\displaystyle\sum_{k=0}^{n}{(3k+1)}$
$=$ $1$ $+\displaystyle\sum_{k=1}^{n}{(3k+1)}$
[$k=0$ は代入して別個で求める。]
$=1+3\displaystyle\sum_{k=1}^{n}{k}+\displaystyle\sum_{k=1}^{n}{1}$
$=1+3\times\displaystyle\frac{1}{2}n(n+1)+n$
$\left[ \displaystyle\sum \text{ の公式を適用} \right]$
$=\displaystyle\frac{1}{2}\left\{2+3n(n+1)+2n\right\}$
$=\displaystyle\frac{1}{2}(3n^2+5n+2)$
$=\displaystyle\frac{1}{2}(n+1)(3n+2)$ (答)
$\sum$ の公式は $\displaystyle\sum_{k=1}^{}{}$ でないと使えないという大きな弱点があります。等差数列の和の公式で求めれば, そんなことを気にせず求められるのでとても簡単!ぜひ習得しましょう!
(3) $\displaystyle\sum_{k=2}^{n-1}{3^{k+1}}$
これはどうしましょうか。流れからもなんとなく分かると思います(笑)
はい,等比数列の和ですね。
等比数列の和は「初項」「公比」「項数」に着目!
ということで,「初項」「公比」「項数」を考えましょう。
$\displaystyle\sum_{k=2}^{n-1}{3^{k+1}}$ なので
初項は $k=2$ を代入したもの
公比は $3$
項数は $(n-1)-2+1=n-2$
ですね。
$\left[\displaystyle\sum_{k=2}^{n-1}{3^{k+1}}=3^3+3^4+\cdots+3^n\right]$
よって,求める和は
初項 $27$,公比 $3$,項数 $n-2$ の等比数列の和より,
$=(\text{初項})\times\displaystyle\frac{(\text{公比})^{(\text{項数})}-1}{(\text{公比})-1}$
[公比が $1$ より大きい場合の公式]
$\displaystyle\sum_{k=2}^{n-1}{3^{k+1}}$
$=27\times\displaystyle\frac{3^{n-2}-1}{3-1}$
$=\displaystyle\frac{27}{2}\left(3^{n-2}-1\right)$ (答)
はい、できました!
等比数列の和について抜けている人は,以下の記事で確認しておきましょう。
答案
(1)
$\displaystyle\sum_{k=1}^{n}{k(4k^2-k+1)}$
$=\displaystyle\sum_{k=1}^{n}{(4k^3-k^2+k)}$
$=4\displaystyle\sum_{k=1}^{n}{k^3}-\displaystyle\sum_{k=1}^{n}{k^2}+\displaystyle\sum_{k=1}^{n}{k}$
$=4\cdot\displaystyle\frac{1}{4}n^2(n+1)^2$
$-\displaystyle\frac{1}{6}n(n+1)(2n+1)$
$+\displaystyle\frac{1}{2}n(n+1)$
$=n^2(n+1)^2$
$-\displaystyle\frac{1}{6}n(n+1)(2n+1)$
$+\displaystyle\frac{1}{2}n(n+1)$
$=\displaystyle\frac{1}{6}n(n+1)\left\{6n(n+1)-(2n+1)+3\right\}$
$=\displaystyle\frac{1}{6}n(n+1)(6n^2+4n+2)$
$=\displaystyle\frac{1}{3}n(n+1)(3n^2+2n+1)$ (答)
(2)
$\displaystyle\sum_{k=0}^{n}{(3k+1)}$
[初項 $1$,末項 $3n+1$,項数 $n+1$ の等差の和より]
$=\displaystyle\frac{1}{2}×(n+1)×\left\{1+(3n+1)\right\}$
$=\displaystyle\frac{1}{2}(n+1)(3n+2)$ (答)
(3)
$\displaystyle\sum_{k=2}^{n-1}{3^{k+1}}$
[初項 $27$,公比 $3$,項数 $n-2$ の等比の和より]
$=27\times\displaystyle\frac{3^{n-2}-1}{3-1}$
$=\displaystyle\frac{27}{2}\left(3^{n-2}-1\right)$ (答)



