ここでは階差数列について説明します。このページの目標は以下です。
階差数列とは何か
$\left\{a_n\right\}$ の階差(隣り合う項の差)を並べた数列 $\left\{b_n\right\}$ を $\left\{a_n\right\}$ の階差数列という。$b_n=a_{n+1}-a_n$ である。

(例) 次の数列 $\left\{a_n\right\}$ の階差数列 $\left\{b_n\right\}$ を考えてみよう。
$1, 2, 6, 15, 31, 56, 92,\cdots$
階差をとってみると,
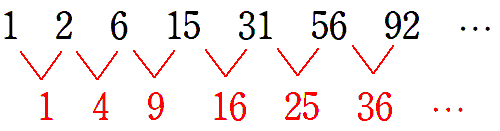
よって,数列 $\left\{a_n\right\}$ の階差数列 $\left\{b_n\right\}$ は
$1, 4, 9, 16, 25, 36, \cdots$
(一般項は $b_n=n^2$)
このように,もとの数列は規則がなくても階差数列を見ると規則が見える場合があります。そして,階差数列 $\left\{b_n\right\}$ の一般項 $b_n$ が分かると,もとの数列 $\left\{a_n\right\}$ の一般項 $a_n$ を求めることができます。その方法について確認していきましょう。
階差数列と一般項(公式)
階差数列から一般項を求める公式
$n\text{≧}2\text{ のとき}$ $a_n=a_1+\displaystyle\sum_{k=1}^{n-1}{b_k}$
公式の導出について(基本)
数列 $\left\{a_n\right\}$ の階差数列が $\left\{b_n\right\}$ であるとき,下のような図をイメージしよう。

この図を見れば,以下のように考えることができますね。
$a_2=$ $a_1$$+$$b_1$
$a_3=$ $a_1$$+$$(b_1+b_2)$
$a_4=$ $a_1$$+$$(b_1+b_2+b_3)$
$a_5=$ $a_1$$+$$(b_1+b_2+b_3+b_4)$
・・・
$a_n=$ $a_1$$+$$(b_1+b_2+\cdots+b_{n-1})$
$(b_1+b_2+\cdots+b_{n-1})$ を $\sum$ を用いて表せば,
$a_n=$ $a_1$ $+$ $\displaystyle\sum_{k=1}^{n-1}{b_k}$
ただし,$a_1$ は階差数列を使って表せない(項が 1 つだと階差が存在しない) ので,この式が成り立つのは $n\text{≧}2$ のときということになります。式で見ても,$n=1$ のとき$\displaystyle\sum_{k=1}^{0}$ となってマズイですね。
公式の導出について(応用)
次のような図をイメージしても導けます。
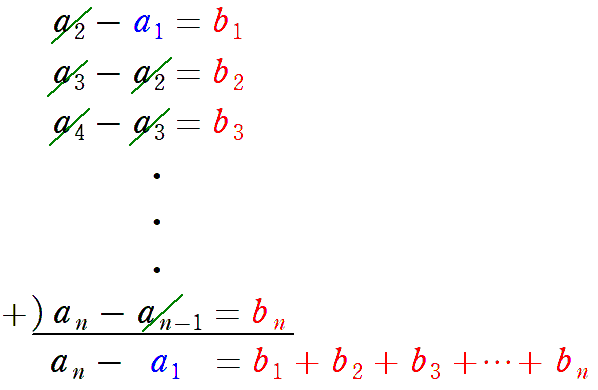
実際に階差数列から一般項を求めるときは,理由1をイメージするのが良いですが,応用問題ではこちらの理由2の理解が重要になるので,どちらも理解しておくことをお勧めします。
階差数列から一般項を求める方法
問題
(1) $1,4,10,22,46,94,\cdots$
(2) $3,5,8,14,25,43,70,\cdots$
解説(授業)
(1) $1,4,10,22,46,94,\cdots$
このままだと規則が分からないので,階差数列 $\left\{b_n\right\}$ を調べてみます
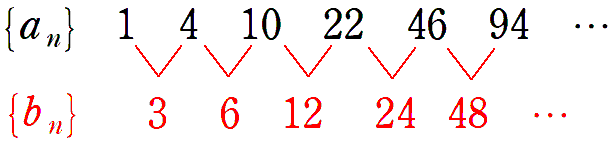
$\left\{b_n\right\}$ が等比数列で,初項と公比から一般項が求まりますね。
初項 $3$,公比 $2$ の等比数列より,$b_n=3\cdot2^{n-1}$
階差数列 $\left\{b_n\right\}$ の一般項さえ求まれば,公式からもとの数列 $\left\{a_n\right\}$ の一般項が求まります。
$n≧2$ のとき
$a_n$ $=$ $a_1$ $+$ $\displaystyle\sum_{k=1}^{n-1}{b_k}$
$=$ $1$ $+$ $\displaystyle\sum_{k=1}^{n-1}{3\cdot2^{k-1}}$
[初項に階差数列を $(n-1)$ 項($1$ 個少ない個数)足す]
$\displaystyle\sum_{k=1}^{n-1}{3\cdot2^{k-1}}$ は等比数列の和で求めるんでしたね。
等比数列の和は,これまで何度も出てきているものですが,求めるために必要なものは何でしょうか。すぐに言えますか?
「初項」「公比」「項数」の $3$ つです。まだすぐ言えないという人は,そろそろ気合を入れて覚えてしまってください!もちろん,公式も含めてです。
$\displaystyle\sum_{k=1}^{n-1}{3\cdot2^{k-1}}$ は初項 $3$,公比 $2$,項数 $n-1$ の等比数列の和なので,
$=(\text{初項})\times\displaystyle\frac{(\text{公比})^{(\text{項数})}-1}{(\text{公比})-1}$
[公比が $1$ より大きい場合の公式]
$\displaystyle\sum_{k=1}^{n-1}{3\cdot2^{k-1}}=3\times\displaystyle\frac{2^{n-1}-1}{2-1}$
よって,
$1$ $+$ $\displaystyle\sum_{k=1}^{n-1}{3\cdot2^{k-1}}$
$=$ $1$ $+$ $3\times\displaystyle\frac{2^{n-1}-1}{2-1}=3\cdot2^{n-1}-2$
したがって,
$a_n=3\cdot2^{n-1}-2$
となりますね。
まだ安心してはいけません。これは,$n≧2$ のときに成り立つことしか言えていないので,$n=1$ でも成り立つことを確認する必要があります。つまり,$a_1=1$ となることを確認します。
$n=1$ を代入すると,
$a_1$ $=3\cdot2^0-2=$ $1$
[$2^0=1$ ( $0$ 乗は必ず $1$ )]
となるので,$n=1$ のときも成り立つことが確認できましたね。
よって,$a_n=3\cdot2^{n-1}-2$ (答)
階差数列から一般項を求めるとき,間違えやすい部分がいくつかあります。慣れるまでは,以下のことに注意しながら解き進めましょう。
・$\displaystyle\sum_{k=1}^{n}$ としてしまう $\left(\text{正しくは}\displaystyle\sum_{k=1}^{n-1}\right)$
・$\displaystyle\sum_{k=1}^{n-1}{3\cdot2^{n-1}}$ のように $n$ のまま $\displaystyle\sum$ に入れてしまう
上記は,注意事項をただ暗記するのでなく,階差数列から一般項は初項に階差数列を $(n-1)$ 項($1$ 個少ない個数)足して求めるという理解をしておくことが重要です。
さらに,以下の記述を忘れないようにしましょう。
・$a_n$ を求めたら $n=1$ で成り立つことを確認する。
(メモで計算して確認し,答案には「これは $n=1$ でも成り立つ」と書いておくだけで十分です)
ちなみに,階差数列から一般項を求めたとき,「$n=1$ のときは成り立たない」という場合はないと考えてください。つまり,$n=1$ のときの結果が初項と一致しなかった場合,計算ミスを疑って欲しい。
(2) $3,5,8,14,25,43,70,\cdots$
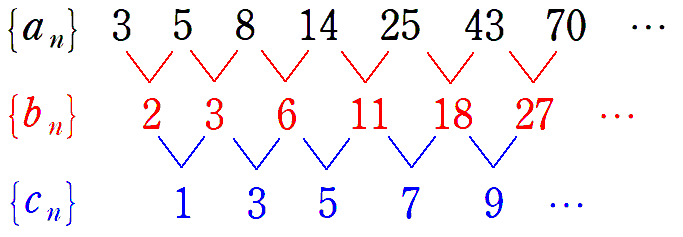
$\left\{a_n\right\}$ の階差数列 $\left\{b_n\right\}$ を調べても規則が見えないので,さらに階差をとって $\left\{c_n\right\}$ を調べてみます。
$\left\{b_n\right\}$ の階差数列 $\left\{c_n\right\}$ を調べることで等差数列が現れますね。
$\left\{a_n\right\}$ を求めるまでの流れは以下のようになります。
$\left\{c_n\right\}$ ($\left\{b_n\right\}$ の階差数列) を求める。
→ $\left\{b_n\right\}$ ($\left\{a_n\right\}$ の階差数列) を求める。
→ $\left\{a_n\right\}$ を求める。
大変そうですが,頑張って求めましょう!
$\left\{c_n\right\}$ は初項 $1$,公差 $2$ の等差数列より
$c_n=1+(n-1)\times2$
よって $c_n=2n-1$
この $c_n$ を使って $b_n$ を求めましょう。
$n\text{≧}2$ のとき
$b_n=b_1+$ $\displaystyle\sum_{k=1}^{n-1}{c_k}$
$=2+$ $\displaystyle\sum_{k=1}^{n-1}{(2k-1)}$
$\displaystyle\sum_{k=1}^{n-1}{(2k-1)}$ は $\sum$ の公式でも求められますが,$k$ の $1$ 次式なので,等差数列の和で求めることもできますね。今回は等差数列の和で計算してみましょう。等差数列の和の求め方はすぐに言えますか?必要なものは何でしょうか。「初項」「末項」「項数」でしたね。
$\displaystyle\sum_{k=1}^{n-1}{(2k-1)}$ は,
初項 $1$ ← $k=1$ を代入したもの
末項 $2n-3$ ← $k=n-1$ を代入したもの
項数 $n-1$ ← $1$ ~ $n-1$
の等差数列の和であるから,
$=\displaystyle\frac{1}{2}\times \text{(項数)}\times \text{(初項+末項)}$
$\displaystyle\sum_{k=1}^{n-1}{(2k-1)}$
$=\displaystyle\frac{1}{2}\times(n-1)\times\left\{1+(2n-3)\right\}$
よって,
$b_n$ $=$ $2$ $+$ $\displaystyle\sum_{k=1}^{n-1}{(2k-1)}$
$=$ $2$ $+$ $\displaystyle\frac{1}{2}\times(n-1)\times\left\{1+(2n-3)\right\}$
$=2+\displaystyle\frac{1}{2}(n-1)(2n-2)$
[$2n-2$ を $2$ でくくって]
$=2+(n-1)^2$
[展開して整理して]
$=n^2-2n+3$
[$b_1=1^2-2\times1+3=2$ で,もとの $b_1$ と一致]
これは,$n=1$ のときも成り立つ。
よって,$b_n=n^2-2n+3$
この $b_n$ を使って $a_n$ を求めましょう。
$n≧2$ のとき
$a_n$ $=a_1+$ $\displaystyle\sum_{k=1}^{n-1}{b_k}$
$=3+$ $\displaystyle\sum_{k=1}^{n-1}{(k^2-2k+3)}$
これを計算するだけなのですが,少し大変そうです。
$\sum$ の公式について確認しておきましょう。
・$\displaystyle\sum_{k=1}^{n}{k}=\displaystyle\frac{1}{2}n\left(n+1\right)$
・$\displaystyle\sum_{k=1}^{n}{k^2}=\displaystyle\frac{1}{6}n\left(n+1\right)(2n+1)$
ですが,今回は $\displaystyle\sum_{k=1}^{n-1}$ なので,$n → n-1$ としたものですね。ただ,書いてみるとややこしい。そこで,これらの公式を以下のように仕組みで覚えて計算しましょう。
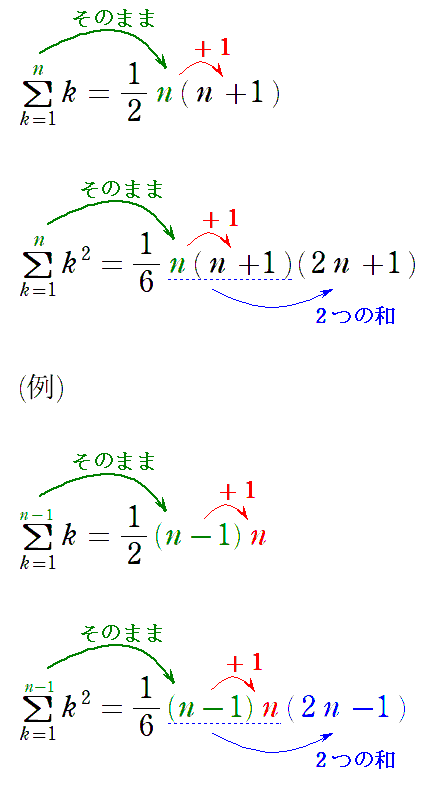
階差数列が絡むと,計算が煩雑になったり,$n=1$ の確認をしたりでどうしても面倒な問題となるため,少しでも単純化し,ミスをしないようにしておきたいですね。
$a_n$ $=3+$ $\displaystyle\sum_{k=1}^{n-1}{(k^2-2k+3)}$
[$\sum$ の公式を適用して]
[数式が切れていたら横にスクロール]
[展開して整理すると]
$=\displaystyle\frac{1}{3}n^3-\displaystyle\frac{3}{2}n^2+\displaystyle\frac{25}{6}n$
[$a_1=\frac{1}{3}-\frac{3}{2}+\frac{25}{6}=3$ より,もとの $a_1$ と一致]
これは,$n=1$ のときも成り立つ。
よって,$a_n= \displaystyle\frac{1}{3}n^3-\displaystyle\frac{3}{2}n^2+\displaystyle\frac{25}{6}n$ (答)
(2) はかなり大変ですが,階差数列から一般項を求める仕組みを理解していれば考え方自体は難しくないはずです。階差数列はこの先も何度も出てくるので,繰り返し解いてしっかり慣れてください。
答案
(1)
$\left\{a_n\right\}$ の階差数列を $\left\{b_n\right\}$ とすると,$\left\{b_n\right\}$ は
$3,6,12,24,48,\cdots$
これは,初項 $3$,公比 $2$ の等比数列より,
$b_n=3\cdot2^{n-1}$
よって,$n≧2$ のとき
$a_n$ $=a_1+$ $\displaystyle\sum_{k=1}^{n-1}{b_k}$
$=1+$ $\displaystyle\sum_{k=1}^{n-1}{3\cdot2^{k-1}}$
[初項 $3$,公比 $2$,項数 $n-1$ の等比の和]
$=1+$ $3\times\displaystyle\frac{2^{n-1}-1}{2-1}$
$=3\cdot2^{n-1}-2$
[$a_1=3\times2^0-2=1$ (メモ)]
これは,$n=1$ のときも成り立つ
∴ $a_n=3\cdot2^{n-1}-2$ (答)
(2)
$\left\{a_n\right\}$ の階差数列を $\left\{b_n\right\}$ とすると,
$2,3,6,11,18,27,・・・$
$\left\{b_n\right\}$ の階差数列を $\left\{c_n\right\}$ とすると,
$1,3,5,7,9,・・・$
$\left\{c_n\right\}$ は,初項 $1$,公差 $2$ の等差数列より,
$c_n=1+(n-1)\times2$
よって $c_n=2n-1$
したがって,$n≧2$ のとき
$b_n=b_1+$ $\displaystyle\sum_{k=1}^{n-1}{c_k}$
$=2+$ $\displaystyle\sum_{k=1}^{n-1}{(2k-1)}$
[$\displaystyle\sum_{k=1}^{n-1}{(2k-1)}$ は初項 1,末項 $2n-3$,項数 $n-1$ の等差の和]
$=2+$ $\displaystyle\frac{1}{2}\times(n-1)\times\left\{1+(2n-3)\right\}$
$=2+(n-1)^2$
$=n^2-2n+3$
[$b_1=1^2-2\cdot1+3=2$ (メモ)]
これは $n=1$ のときも成り立つ
よって $b_n=n^2-2n+3$
したがって,$n≧2$ のとき
$a_n$ $=a_1+$ $\displaystyle\sum_{k=1}^{n-1}{b_k}$
$=3+$ $\displaystyle\sum_{k=1}^{n-1}{(k^2-2k+3)}$
[数式切れていたら横にスクロール]
$=\displaystyle\frac{1}{3}n^3-\displaystyle\frac{3}{2}n^2+\displaystyle\frac{25}{6}n$
[$a_1=\frac{1}{3}-\frac{3}{2}+\frac{25}{6}=3$ (メモ)]
これは,$n=1$ のときも成り立つ。
よって $a_n= \displaystyle\frac{1}{3}n^3-\displaystyle\frac{3}{2}n^2+\displaystyle\frac{25}{6}n$ (答)

