数列の和Snが与えられているときの一般項a_nの求め方

数列の和 $S_n$ が与えられているとき，一般項 $a_n$ を求める方法について説明します。

数列の和と一般項の関係について(公式)

和と一般項の関係の公式の導出

[1] は当たり前だよね。$S_1$ は 第 1 項までの和であるから初項 $a_1$ と一致します。当たり前で簡単な式ですが，必ず使うので軽視しないように。
[2] も式の意味を考えれば当たり前なんだけど，数式で意味を確認しながら導出してみましょう。

$n≧2$ のとき
$S_n$ $=$ $a_1+a_2+a_3+･･･+a_{n-1}$ $+$ $a_n$
　 $=$ $S_{n-1}$ $+$ $a_n$
よって　$a_n$ $=$ $S_n$ $-$ $S_{n-1}$

下のようにイメージして，「1 つ手前までの和を引く」と理解しておきましょう。ここで考える問題は公式の丸暗記でも対応できますが，応用問題やこの先に出てくる漸化式では，丸暗記だと少し解きにくいものが出てくるので，意味を理解することが重要です。

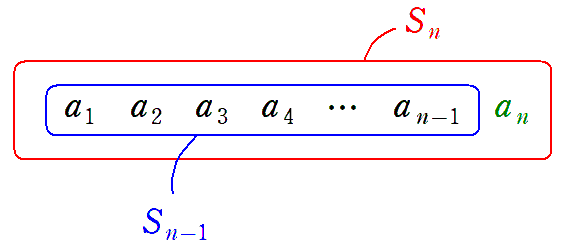
$n=1$ のとき $S_0$ が現れておかしいことになるので，$n≧2$ のときという条件が入ります。（ $a_1$ には手前が存在しない）

和 $S_n$ から一般項 $a_n$ を求める問題の解き方

問題

解説（授業）

数列の和が式で与えられているときは，数列の和と一般項の関係を使う問題だと考えよう。つまり，
[1] ($n=1$ のとき) $a_1=S_1$
[2] $n≧2$ のとき $a_n=S_n-S_{n-1}$
この２式を利用します。

[1] により $n=1$ のときの $a_n$ が求まり，
[2] により $n≧2$ のときの $a_n$ が求まる
という意識をもっておきましょう。

(1) $S_n=2n^2-3n$
$a_1=S_1$
　 $=2･1^2-3･1=-1$
よって　$a_1=-1$　･･･①
これが $n=1$ のときの $a_n$ ですね。

$n≧2$ のとき
$a_n=$ $S_n$ $-$ $S_{n-1}$
$S_n=2n^2-3n$
$S_{n-1}$ $=$ $\left\{2(n-1)^2-3(n-1)\right\}$
　　$=2n^2-7n+5$
であるから，
$a_n$ $=$ $(2n^2-3n)$ $-$ $(2n^2-7n+5)$
　 $=4n-5$
よって　$a_n=4n-5$ ($n≧2$) ･･･②

[1] と [2] により得られたものを確認しましょう。
$a_1=-1$　･･･①
$a_n=4n-5$ ($n≧2$)　･･･②
すなわち $a_n=\begin{cases}-1 \enspace(n=1)\\4n-5 \enspace(n≧2)\end{cases}$ ですね。
ここで，②の式に $n=1$ を代入すると
$a_1=4\times1-5=-1$
となり，①と一致します。
これは，② の式は $n=1$ のときも成り立つということになるので，ひとつにまとめて，
$a_n=4n-5$ (答)
となります。

(2) $S_n=5^n$
方針は (1) と同じで良いですね。

$a_1=S_1$
　 $=5^1$
　 $=5$
よって　$a_1=5$　･･･①

$n≧2$ のとき
$a_n=$ $S_n$ $-$ $S_{n-1}$
　 $=$ $5^n$ $-$ $5^{n-1}$
[指数を $n-1$ (小さい方) にそろえて]
　 $=5\times5^{n-1}-5^{n-1}$
[$5^{n-1}$ でくくって]
　 $=5^{n-1}(5-1)$
　 $=4･5^{n-1}$
よって　$a_n=4･5^{n-1}$ ($n≧2$)･･･②

②に $n=1$ を代入すると，
$a_1=4\times5^0=4\times1=4$
となり，①と一致しない。つまり，②は $n=1$ のときは成り立たないということになります。
よって，(1) のようにまとめることができないため，次のように，$n=1$ と $n≧2$ を分けて答えます。
$a_n=\begin{cases}5\enspace(n=1)\\4･5^{n-1} \enspace(n≧2) \end{cases}$　(答)

答案

(1)
$S_n=2n^2-3n$

$a_1=S_1$
　 $=2･1^2-3･1$
　 $=-1$

∴ $a_1=-1$　･･･①

$n≧2$ のとき

$a_n=$ $S_n$ $-$ $S_{n-1}$

　 $=$ $(2n^2-3n)$
　　　$-$ $\left\{2(n-1)^2-3(n-1)\right\}$

　 $=(2n^2-3n)-(2n^2-7n+5)$
　 $=4n-5$

∴ $a_n=4n-5$ ($n≧2$) ･･･②

ここで，②において $n=1$ を代入すると，

$a_1=4･1-5=-1$

となり，①と一致する。つまり，②は $n=1$ のときも成り立つ。

以上より，

$a_n=4n-5$　(答)

(2)
$S_n=5^n$

$a_1=S_1$
　 $=5^1$
　 $=5$

∴ $a_1=5$　･･･①

$n≧2$ のとき

$a_n=$ $S_n$ $-$ $S_{n-1}$
　 $=$ $5^n$ $-$ $5^{n-1}$
　 $=5^{n-1}(5-1)$
　 $=4･5^{n-1}$

∴ $a_n=4･5^{n-1}$ ($n≧2$) ･･･②

ここで，②において $n=1$ を代入すると，

$a_1=4･5^0=4$

となり，①と一致しない。つまり，②は $n=1$ のときは成り立たない。

以上より，

$a_n=\begin{cases}5 \enspace(n=1)\\4\cdot5^{n-1} \enspace(n≧2) \end{cases}$　(答)

和 $S_n$ と一般項 $a_n$ の問題がこれで「解ける！」