$\displaystyle\sum_{k=1}^{n}\frac{1}{k}$,$\displaystyle\sum_{k=1}^{n}\frac{1}{k^2}$,$\displaystyle\sum_{k=1}^{n}\frac{1}{\sqrt{k}}$
$\displaystyle\sum_{k=1}^{n}\log_{}{k}$,$\displaystyle\sum_{k=1}^{n}k\log_{}{k}$
などを見たら
グラフをかいて
面積ではさむ!
長方形でダメなら台形で!
$\displaystyle\sum_{k=1}^{n}\frac{1}{k}$,$\displaystyle\sum_{k=1}^{n}\frac{1}{k^2}$,$\displaystyle\sum_{k=1}^{n}\frac{1}{\sqrt{k}}$,$\displaystyle\sum_{k=1}^{n}\log_{}{k}$,$\displaystyle\sum_{k=1}^{n}k\log_{}{k}$ などを見たら
グラフをかいて面積ではさむ
(例)$\displaystyle\sum_{k=1}^{n}\frac{1}{k}$
$y=\displaystyle\frac{1}{x}$ のグラフをかく
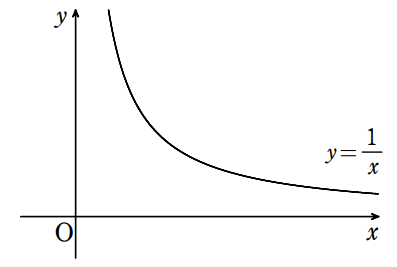
$x=k$,$x=k+1$ により囲まれる部分の面積は $\displaystyle\int_{k}^{k+1}\frac{1}{x}\space dx$

$2$ つの長方形の面積ではさむ
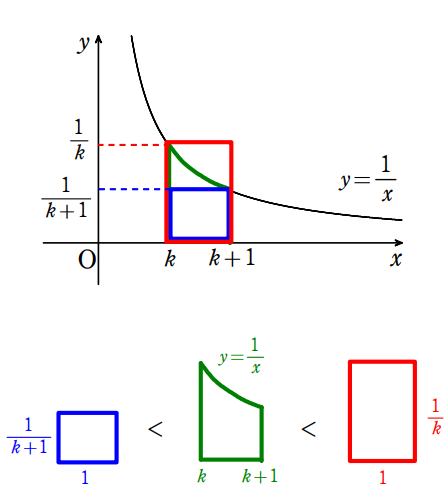
$\displaystyle\frac{1}{k+1}$ $<$ $\displaystyle\int_{k}^{k+1}\frac{1}{x}\space dx$ $<$ $\displaystyle\frac{1}{k}$
こんな具合です。この不等式をパパっと作れるようにしておきましょう。
$\displaystyle\sum_{k=1}^{n}\frac{1}{k}$,$\displaystyle\sum_{k=1}^{n}\frac{1}{k^2}$,$\displaystyle\sum_{k=1}^{n}\frac{1}{\sqrt{k}}$,$\displaystyle\sum_{k=1}^{n}\log_{}{k}$,$\displaystyle\sum_{k=1}^{n}k\log_{}{k}$
もしくはこれと似たようなものがあれば上記のように面積ではさみ,不等式を作るのが定石です。
いくつか注意点です。
$\sum$ を使われていないときも同じ
当たり前ですが,$\sum$ を使わずに表される場合でも同じです。
| $\sum$ あり | $\sum$ なし |
|---|---|
| $\displaystyle\sum_{k=1}^{n}\frac{1}{k^2}$ | $\displaystyle\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots+\frac{1}{n^2}$ |
| $\displaystyle\sum_{k=1}^{n}\log_{}{k}$ | $\displaystyle\log_{}{1}+\log_{}{2}+\cdots+\log_{}{n}$ $=$ $\displaystyle\log_{}{(n!)}$ |
| $\displaystyle\sum_{k=1}^{n}k\log_{}{k}$ | $\displaystyle1\log_{}{1}+2\log_{}{2}+\cdots+n\log_{}{n}$ $=$ $\displaystyle\log_{}{\left(1^1 ・ 2^2 ・ \cdots ・ n^n \right)}$ |
特に,$\displaystyle\sum_{k=1}^{n}\log_{}{k}$ は $\displaystyle\log_{}{(n!)}$ と表現されることが多い。同値変形を見落とさないようにすること。
先の小問に現れたときでも実行
例えば (2) で初めて $\displaystyle\sum_{k=1}^{n}\frac{1}{k}$ が問題文に出てきたとしても,(1) が (2) の誘導になっている場合が多い。つまり,(1) が「グラフをかいて面積ではさむ」ことで解ける場合がある。大問全体を見て,どこかに $\displaystyle\sum_{k=1}^{n}\frac{1}{k}$ などがあれば,(1) の時点で面積ではさむ作業を行いましょう。
例題1「長方形と長方形ではさむ」(基本)
$\enspace$ $n$ を $2$ 以上の自然数とする。次の問いに答えよ。
(1)$\enspace$次の不等式が成り立つことを示せ。
| $n\log_{}{n}-n+1<\displaystyle\sum_{k=1}^{n}\log_{}{k}<(n+1)\log_{}{n}-n+1$ |
(2)$\enspace$次の極限値を求めよ。$$\displaystyle\lim_{n\rightarrow\infty} \frac{\log_{}{(n!)}}{n\log_{}{n}}$$
(1) $\displaystyle\sum_{k=1}^{n}\log_{}{k}$ があるので,グラフをかいて面積ではさむのが定石ですね。
一応,触れておきますが,「$2$ 以上のすべての自然数で成り立つ」証明なので「数学的帰納法」も定石と言えます。((参考)【証明問題】対偶法、背理法、数学的帰納法はいつ使う?)
このように複数の定石が重なった場合は,いずれかの定石で進めて,上手くいかなければ他の定石で進めてください。多くの場合は,どの定石で進めても解けますが,ある定石が簡単だったり,ある定石では解けなかったりということもあります。もちろん,複数の定石を組み合わせて解く問題もあります。
今回は「$\displaystyle\sum_{k=1}^{n}\log_{}{k}$」に着目した場合の定石を考えます。
解答のように面積ではさむことにより,
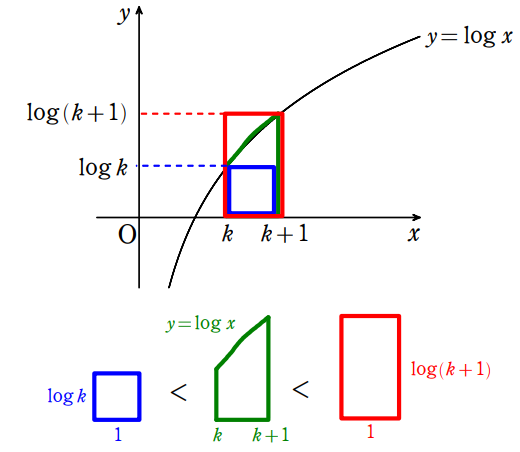
$\displaystyle\log_{}{k}$ $<$ $\displaystyle\int_{k}^{k+1}\log_{}{x} \space dx$ $<$ $\log_{}{k+1}$$\enspace \cdots \text{(☆)}$
を得ます。そして,次の流れも定石として覚えておきましょう。
(☆) に $k=1,2,\cdots,n-1$ を代入して辺々足すと,(左辺) $<$ (中辺) より
$\displaystyle\log_{}{1}+\log_{}{2}+\cdots+\log_{}{(n-1)}$ $<$ $\displaystyle\int_{1}^{n}\log_{}{x} \space dx$
$\displaystyle\left(\int_{1}^{2}+\int_{2}^{3}+\cdots+\int_{n-1}^{n}=\int_{1}^{n}\text{ より}\right)$
あとは,$\displaystyle\int_{1}^{n}\log_{}{x} \space dx$ を計算しつつ,証明したい式に寄せていくだけです。少し慣れが必要ですが,難しくはありません。
次に,(☆) の (中辺) $<$ (右辺) を見て,同じことをすれば,残りの不等式が示されます。計算は解答の通りですが,一度,自分の手で計算してみましょう。
このように (☆) に $k=1,2,\cdots,n-1$ を代入して辺々足すのを定石としておいてください。今回は $k=1,2,\cdots,n-1$ を代入しましたが,代入していく値は問題によって変わります。$$k=1,2,\cdots,n$$ $$k=\displaystyle\frac{1}{2},\frac{3}{2},\cdots,\frac{2n-1}{2}$$
などの場合もあります。示したい式から判断してください。
(2) はさみうちの原理から求めます。かなり基本的な話ですが「不等式のあとの極限」は「はさみうちの原理」は定石です。知らなかったという人は覚えておいてください。特に難しい計算はありません。
例題2「長方形と台形ではさむ」(応用)
$\enspace$次の不等式を証明せよ。ただし,$n$ は自然数とする。
(1)
| $\space \displaystyle\frac{1}{k+1}<\int_{k}^{k+1}\frac{1}{x}\space dx<\frac{1}{2}\left(\frac{1}{k}+\frac{1}{k+1}\right)$ |
(2)
| $\space\displaystyle 1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}-\log_{}{n}>\frac{1}{2}$ |
(1) を考える前に,(2) を見ましょう。(2) の左辺に $\displaystyle\sum_{k=1}^{n}\frac{1}{k}$ を含んでいますね。
よって,グラフをかいて面積ではさむのが定石です。
しかし,問題が生じます。例題1と同様に 2 つの長方形ではさむと,
$\displaystyle\frac{1}{k+1}$ $<$ $\displaystyle\int_{k}^{k+1}\frac{1}{x}\space dx$ $<$ $\displaystyle\frac{1}{k}$
が得られます。与えられた不等式の (左辺) $<$ (中辺) は示せますが,ここからどう頑張っても (中辺) $< $(右辺) が示せません。
これは,長方形ではさむと評価が甘すぎたということです。よって,もっと厳しく評価する必要があります。どうすれば良いかというと長方形ではなく「台形」ではさみます。
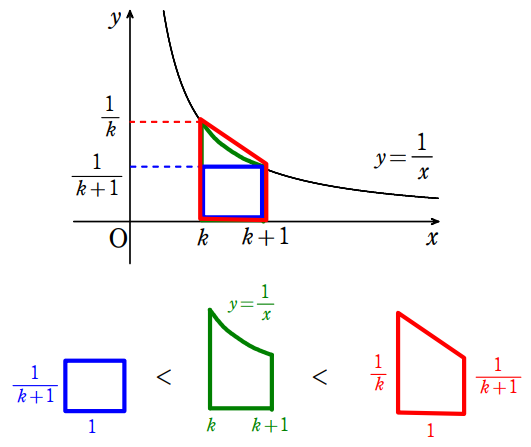
台形ではさんだ方が厳しく評価できていることが分かるでしょうか。まずは長方形ではさんでみて「長方形でダメなら台形で」はさみましょう。
あとは例題1と同じ流れです。(やや計算が煩雑ですが)
おまけ「台形と台形ではさむ」(発展)
例題2の延長でできそうな気がするかもしれませんが,実際に図をかいてみると厄介であることが分かります。
台形と台形ではさもうとすると,2 個目の台形がうまく作れないと思います。ここが厄介なのです。
ひとまずは例題1と例題2のレベルをしっかりできるように演習してください。ほとんどの問題はそれで対応可能です。後日,難関大学志望者向けに「台形と台形ではさむ」パターンの問題を記事にします。

