∑（シグマ）の公式と∑の計算全パターン。すべての∑に対応するための考え方

∑の計算全パターン

　まずは $∑$ のパターンをすべて頭に入れましょう。

パターン	例	求め方
$∑(\text{等差})$	$\displaystyle\sum_{k=0}^{n+1}(2k+3)$	等差数列の和の公式
$∑(\text{等比})$	$\displaystyle\sum_{k=0}^{n}2^k$	等比数列の和の公式
$∑(3\text{ 次以下の整式})$	$\displaystyle\sum_{k=1}^{n}(3k^2+k-4)$	$∑$ の公式
$∑(\text{等差})・(\text{等比})$ $∑(k の 2\text{ 次式})・(\text{等比})$	$\displaystyle\sum_{k=1}^{n}2k・3^{k-1}$	公比をかけたものを ずらして引く
$∑{}_n\text{C}_r$	$\displaystyle\sum_{k=1}^{n}{}_n\text{C}_k$ $\displaystyle\sum_{k=1}^{n}\frac{n!}{k!(n-k)!}$	二項定理
$∑(\text{階差})$ (上記以外はこれ！)	$\displaystyle\sum_{k=1}^{n}(a_{k+1}-a_k)$ $\displaystyle\sum_{k=1}^{n}\frac{1}{k(k+2)}$	書き出して 打ち消し合わせる

※数Ⅲを含めると，パターンが増えます。（(参考)【数学Ⅲ】Σ(k/1),Σ(1/k^2),Σ(1/√k),Σlogk,Σklogkなどを見たら90%すること）

　$∑$ の計算が必要になった際，上記のことを頭に入れて臨む必要があります。「なんとなくできた」ではダメです。明確な根拠をもって計算してください。応用問題は $∑(\text{階差})$ であることが多いです。基本的には上から確認していきます。

「等差や等比」じゃなければ「$∑$ の公式」
→「$∑$ の公式」でもなければ「(等差)・(等比)」
→「(等差)・(等比)」でもなければ「${}_n\text{C}_r$」
→「${}_n\text{C}_r$」でもなければ「階差」

　という感じ。それぞれの求め方について簡単に触れていきますが，あくまでも $Σ$ の考え方を伝えるのが主な目的であるため，問題は基本的なものにとどめておきます。考え方を理解した上で，問題集を用いて演習しましょう。

$∑(\text{等差})$ は等差数列の和の公式！

（例）$\displaystyle\sum_{k=0}^{n+1}(2k+3)$　解答

　実は意外と差がつきます。これを $∑$ の公式で頑張って求めようとしてはいけません。$1$ 次式は等差数列なので等差数列の和の公式で求めてください。

初項	$k=0$ 代入して	$3$
末項	$k=n+1$ 代入して	$2n+5$
項数	$0$ ～ $n+1$ より	$n+2$

　初項，末項，項数をそれぞれ求めて等差数列の和の公式を使って終わり。
　項数は間違えやすいので注意！
　「$a$ ～ $b$ 」の個数は 「$b$ – $a$ + 1」
　この +1 を忘れやすい！

$∑(\text{等比})$ は等比数列の和の公式！

（例）$\displaystyle\sum_{k=0}^{n}2^k$　解答

これは等比数列の和の公式一択ですね。

初項	$k=0$ 代入して	$1$
公比	$2^k$ より	$2$
項数	$0$ ～ $n$ より	$n+1$

$∑(3\text{ 次以下の整式})$ は∑の公式！

（例）$\displaystyle\sum_{k=1}^{n}(3k^2+k-4)$　解答

　等差数列でも等比数列もないとき，初めて $∑$ の公式の出番です！

[１] $\displaystyle\sum_{k=1}^{n}{c}=cn$

[２] $\displaystyle\sum_{k=1}^{n}{k}=\displaystyle\frac{1}{2}n\left(n+1\right)$

[３] $\displaystyle\sum_{k=1}^{n}{k^2}=\displaystyle\frac{1}{6}n\left(n+1\right)(2n+1)$

[４] $\displaystyle\sum_{k=1}^{n}{k^3}=\left\{\displaystyle\frac{1}{2}n\left(n+1\right)\right\}^2$

　　　　　　$=\displaystyle\frac{1}{4}n^2\left(n+1\right)^2$

　公式を使えば終わり！…ですが，公式はしっかり覚えていますか？覚えにくい[２] と [３]について，正しい覚え方を図にしたので参考にしてください。

$∑(\text{等差})・(\text{等比})$は公比をかけたものをずらして引く！

（例）$\displaystyle\sum_{k=1}^{n}2k・3^{k-1}$　解答

　ここからは応用問題です。「等差の和」「等比の和」「$∑$ の公式」いずれも使えません。そんなときは式をよく観察しましょう。この問題は $∑(\text{等差})・(\text{等比})$ という形になっています。これは「公比をかけたものをずらして引く」のが定石です。

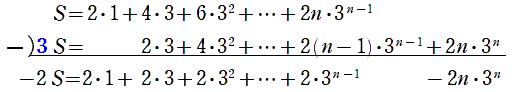
こんな感じですね。

　これの亜種として $∑(k の 2\text{ 次式})・(\text{等比})$ もあります。同じ手順で求められます。

　それと次の式も今回のパターンです。

　$\displaystyle\sum_{k=1}^{n}{\displaystyle\frac{k+1}{2^k}}$

　分かりますか？

$\displaystyle\frac{k+1}{2^k}=$$(k+1)$ $\cdot$ $\left(\displaystyle\frac{1}{2}\right)^k$

　と見れば $(\text{等差})・(\text{等比})$ ですね。パターンを意識しておかないと見落としそうです。

$∑{}_n\text{C}_r$ は二項定理！

（例）$\displaystyle\sum_{k=1}^{n}{}_n\text{C}_k$ ，　$\displaystyle\sum_{k=1}^{n}\frac{n!}{k!(n-k)!}$　解答

${}_n\text{C}_k=\displaystyle\frac{n!}{k!(n-k)!}$ なのでどちらも同じです。

　ちょっとマニアックなパターンですが，知らないと手に負えないのでしっかり押さえておきましょう。

　${}_n\text{C}_r$ の和は $(1+x)^n$ を二項定理で展開するのが定石です。

$$(1+x)^n={}_n\text{C}_0+{}_n\text{C}_1 x+\dots+{}_n\text{C}_n x^n$$

この式に $x=1$ など代入して，あとは求めたいものを見比べて考えればOKです！

$(1+x)^n$ の $n$ は ${}_n\text{C}_r$ の $n$ に対応しています。$\displaystyle\sum_{k=1}^{9}{}_{10}\text{C}_k$ であれば $(1+x)^{10}$ で二項定理です。

$∑(\text{階差})$ は書き出して打ち消し合わせる！

（例）$\displaystyle\sum_{k=1}^{n}\frac{1}{k(k+2)}$　解答

　部分分数分解で求める典型的な和の計算ですね。部分分数分解することにより「階差」の形を作り出します。ちなみに，$∑(\text{階差})$ を求めるときのイメージは下の図の通りです。

　「部分分数分解」や「有理化」によって，このパターンに持ち込むのは基本問題ですね。数列分野においては，次の部分分数分解の式を公式として覚えておきましょう。

　$\displaystyle\frac{1}{AB}=\displaystyle\frac{1}{B-A}\left(\displaystyle\frac{1}{A}-\displaystyle\frac{1}{B}\right)$

　$\displaystyle\frac{1}{ABC}=\displaystyle\frac{1}{C-A}\left(\displaystyle\frac{1}{AB}-\displaystyle\frac{1}{BC}\right)$

どのパターンにも当てはまらないときは？（ここからが最重要）

　この先，学習や受験において，$∑$ の式を見て「どのパターンにも当てはまらなくない？」なんてときがくると思います。難しい大学であればあるほど，その可能性は高いでしょう。このときに対応できるかどうかで大きな差がつきます。

「該当なし」はすべて「階差」に持ち込む！

　はい，もう全部「階差」です。パターンの見落としがないことを確認したら，全力で「階差」に持ち込む努力をしてください。全神経を注ぎ込みましょう。パターンの把握は，そのパターンの計算ができるようになる上でも必要ですが「階差に持ち込むしかない」ことを見抜くためにも重要なのです。

経験がないと難しい「階差」に持ち込む例題

　とはいえ，慣れていなかったり経験がなかったりすると難しいものもあるので，紹介しておきます。一度，自分で考えてみましょう！

まとめ

　数Ⅲを含めると，$\sum$ のパターンが増えます。